Unlock Insights with Cluster-Graph Hybrid

In an era defined by an unprecedented deluge of data, the ability to extract meaningful, actionable insights has become the cornerstone of innovation, competitive advantage, and informed decision-making across virtually every sector. From the intricate web of social interactions to the complex pathways of biological systems, and from the nuanced patterns of financial transactions to the sprawling architectures of urban planning, data presents both a colossal challenge and an immense opportunity. Traditional analytical paradigms, while powerful in their own right, often grapple with the sheer volume, velocity, and variety of modern datasets, frequently falling short in uncovering the deep, interconnected truths that lie beneath the surface. The limitations often stem from a compartmentalized view of data – either focusing on similarities within groups or relationships between entities, but rarely synthesizing both perspectives holistically.

This deficiency has spurred a relentless quest for more sophisticated analytical methodologies, leading us to the burgeoning field of hybrid data models. Among these, the Cluster-Graph Hybrid approach stands out as a transformative paradigm, offering a powerful synergy that transcends the individual limitations of its constituent parts. By meticulously integrating the principles of cluster analysis, which excels at identifying inherent groupings and structures within data based on similarity, with the robust framework of graph theory, which is adept at modeling relationships and interactions between discrete entities, this hybrid model unlocks a richer, more contextualized understanding of complex systems. It moves beyond merely seeing the trees or the forest, enabling us to discern both the individual species within the forest (clusters) and the intricate ecological network that binds them together (graphs), revealing a tapestry of insights previously obscured. This article delves deep into the foundational concepts, architectural considerations, and practical applications of the Cluster-Graph Hybrid approach, highlighting its potential to revolutionize how we perceive and interact with data, while also exploring the crucial role of advanced protocols like the Model Context Protocol (MCP) and indispensable infrastructure such as LLM Gateway solutions in its successful implementation and scalable deployment.

The Foundations: Understanding Clustering and Its Power

Clustering, at its core, is an unsupervised machine learning technique aimed at grouping a set of objects in such a way that objects in the same group (cluster) are more similar to each other than to those in other groups (clusters). This fundamental concept underpins a vast array of analytical tasks, from market segmentation in business to anomaly detection in cybersecurity, and from image segmentation in computer vision to genomic analysis in bioinformatics. Its power lies in its ability to discover intrinsic structures and patterns within data without prior knowledge of those patterns, essentially allowing the data to speak for itself regarding its natural groupings.

The importance of clustering in pattern recognition cannot be overstated. In high-dimensional datasets where visual inspection is impossible, clustering algorithms act as powerful exploratory tools, revealing hidden categories that might otherwise remain undetected. For instance, in a dataset of customer purchasing habits, clustering might reveal distinct segments of customers with similar preferences, enabling targeted marketing strategies. In network security, unusual clusters of network activity could signal a potential cyber threat. The efficacy of clustering, however, is heavily reliant on the chosen algorithm and the definition of "similarity" or "distance" between data points. Common distance metrics include Euclidean distance for continuous data, cosine similarity for text data, or Jaccard similarity for binary data. The choice of metric is paramount, as it directly influences how clusters are formed and the quality of the insights derived.

Several prominent clustering algorithms have evolved, each with its unique strengths and weaknesses, making the selection process a critical decision based on the specific characteristics of the data and the analytical objectives.

K-means Clustering: Simplicity and Efficiency

K-means is arguably the most widely used clustering algorithm due to its simplicity, efficiency, and scalability for large datasets. It works by iteratively partitioning n data points into k clusters, where k is a predefined number. The algorithm proceeds by: 1. Initialization: Randomly selecting k initial cluster centroids. 2. Assignment: Assigning each data point to the nearest centroid, forming k clusters. 3. Update: Recalculating the centroids as the mean of all data points assigned to that cluster. 4. Iteration: Repeating steps 2 and 3 until the centroids no longer change significantly, or a maximum number of iterations is reached.

While K-means is fast and easy to implement, it has certain limitations. Its performance is highly sensitive to the initial choice of centroids, often leading to different results on different runs. It struggles with non-globular clusters and varying cluster sizes or densities, as it implicitly assumes clusters are convex and of similar variance. Moreover, the necessity to pre-specify k (the number of clusters) is a significant challenge, often requiring domain expertise or auxiliary methods like the elbow method or silhouette analysis to determine an optimal value.

Hierarchical Clustering: A Tree of Relationships

Hierarchical clustering builds a hierarchy of clusters, represented as a dendrogram (a tree-like diagram). It can be broadly categorized into two types: * Agglomerative (Bottom-up): Each data point starts as its own cluster, and pairs of clusters are merged iteratively until all data points belong to a single cluster. The merging decision is based on a linkage criterion (e.g., single linkage, complete linkage, average linkage), which defines the distance between two clusters. * Divisive (Top-down): All data points start in one cluster, and the cluster is recursively split until each data point is its own cluster. This approach is computationally more intensive than agglomerative methods.

The primary advantage of hierarchical clustering is that it does not require a pre-specified number of clusters k. The dendrogram provides a rich visualization of the cluster hierarchy, allowing analysts to choose a suitable number of clusters by cutting the tree at a certain level. However, it can be computationally expensive for very large datasets, as it typically requires calculating and storing a similarity matrix of all pairs of data points. Additionally, once a merge or split is made, it cannot be undone, which can lead to suboptimal clustering decisions.

DBSCAN: Discovering Arbitrary Shapes

Density-Based Spatial Clustering of Applications with Noise (DBSCAN) is a powerful algorithm that can discover clusters of arbitrary shape and detect outliers. Instead of assuming spherical clusters like K-means, DBSCAN groups together points that are closely packed together, marking as outliers points that lie alone in low-density regions. It defines clusters based on two parameters: * epsilon (ε): The maximum radius of the neighborhood. * MinPts: The minimum number of points required to form a dense region.

DBSCAN classifies points into three categories: * Core Points: A point that has at least MinPts within its ε-neighborhood. * Border Points: A point that has fewer than MinPts within its ε-neighborhood but is in the ε-neighborhood of a core point. * Noise Points: A point that is neither a core point nor a border point.

A cluster is formed by connecting all core points that are density-reachable from each other, along with their associated border points. DBSCAN's strengths include its ability to identify arbitrarily shaped clusters and its robustness to noise. However, it struggles with varying densities within the data and choosing optimal ε and MinPts can be challenging and domain-dependent.

Spectral Clustering: Leveraging Graph Theory

Spectral clustering is a modern technique that leverages the properties of graphs to perform clustering. It transforms the clustering problem into a graph partitioning problem. The data points are represented as nodes in a similarity graph, where edges connect similar points, and edge weights reflect the degree of similarity. The algorithm then uses the eigenvalues and eigenvectors of the graph's Laplacian matrix to reduce the dimensionality of the data before applying a standard clustering algorithm (like K-means) in the transformed space.

This method is particularly effective for discovering complex, non-convex clusters that are well-separated but not easily identifiable by distance-based methods. Its strength lies in its ability to capture the global structure of the data through the graph representation. However, it can be computationally intensive for very large datasets due to the eigen-decomposition step, and the construction of the similarity graph itself can be a non-trivial task, requiring careful selection of similarity metrics and neighborhood definitions.

Challenges and the Need for Augmentation

While clustering techniques are invaluable, they face inherent challenges. The "curse of dimensionality" can degrade performance in high-dimensional spaces, where data points become increasingly sparse, making distance metrics less meaningful. Defining an appropriate similarity measure is often complex and domain-specific. Furthermore, many algorithms struggle with noise and outliers, which can distort cluster boundaries. Most importantly, clustering primarily focuses on grouping by similarity, often overlooking the explicit relationships between data points or between the clusters themselves. This is precisely where graph structures offer a crucial augmentation, paving the way for the sophisticated Cluster-Graph Hybrid models. Clustering can act as a powerful pre-processing step, simplifying the data for graph analysis by grouping similar entities or identifying initial communities, thus setting the stage for deeper, relationship-aware insights.

The Power of Graph Structures: Unveiling Connections

While clustering methods excel at identifying latent groupings within data, they often operate under an implicit assumption that data points are largely independent entities whose similarities can be directly computed. This perspective, however, falls short when the explicit relationships and interactions between data points are not just incidental but are, in fact, the primary drivers of underlying phenomena. This is where graph structures emerge as an indispensable analytical tool, offering a natural and intuitive framework for modeling and understanding interconnected systems. A graph, in its simplest form, is a collection of nodes (or vertices) representing entities and edges (or links) representing relationships between these entities.

The essence of graph theory lies in its ability to explicitly represent connections. Consider a social network: individuals are nodes, and friendships are edges. In a biological network, proteins are nodes, and their interactions are edges. In a financial system, accounts are nodes, and transactions are edges. This explicit representation of relationships allows for a deeper level of analysis that goes beyond mere attribute similarity, delving into the structural properties and flow dynamics within the system.

Fundamental Elements and Types of Graphs

Graphs are incredibly versatile and can be categorized based on various properties: * Nodes (Vertices): The fundamental entities in a graph. These could be people, computers, documents, genes, cities, or any discrete unit of interest. * Edges (Links): The connections or relationships between nodes. Edges can represent friendships, communications, transactions, dependencies, or spatial proximity.

Based on the nature of their edges, graphs can be: * Undirected Graphs: Edges have no direction, meaning the relationship is symmetrical (e.g., friendship on Facebook: if A is friends with B, B is friends with A). * Directed Graphs: Edges have a specific direction, indicating an asymmetrical relationship (e.g., follower on Twitter: A follows B does not necessarily mean B follows A). * Weighted Graphs: Edges have numerical values (weights) associated with them, representing the strength, cost, duration, or capacity of the relationship (e.g., traffic volume between two cities, frequency of communication). * Bipartite Graphs: Nodes can be divided into two disjoint sets, and edges only connect nodes from one set to nodes from the other set (e.g., users and movies, where edges indicate a user has watched a movie). * Multigraphs: Allow multiple edges between the same pair of nodes (e.g., different types of relationships between two people).

The choice of graph type is crucial as it dictates the kind of information that can be encoded and subsequently extracted through graph analysis.

Core Graph Analytics Fundamentals

Graph analytics provides a rich toolkit for interrogating the structure and dynamics of networks. Key analytical techniques include:

1. Centrality Measures: These metrics quantify the importance or influence of nodes within a network.
   • Degree Centrality: The number of edges connected to a node. High degree indicates a highly connected node, often acting as a hub.
   • Betweenness Centrality: Measures the extent to which a node lies on the shortest paths between other nodes. High betweenness suggests a node is critical for information flow, acting as a "bridge."
   • Closeness Centrality: Measures how "close" a node is to all other nodes in the network, calculated as the inverse of the sum of the shortest path distances from a node to all other nodes. High closeness indicates a node that can quickly spread information.
   • Eigenvector Centrality: Assigns relative scores to all nodes in the network based on the principle that connections to high-scoring nodes contribute more to the score of the node in question. This is particularly useful for identifying influential nodes in networks where influence is transitive.
2. Community Detection: The process of identifying groups of nodes that are more densely connected within themselves than with nodes outside the group. These "communities" or "modules" often represent functional units, social groups, or thematic clusters within the network. Algorithms like Louvain method, Girvan-Newman, or Infomap are commonly used for this purpose.
3. Pathfinding Algorithms: Used to find the shortest or most optimal path between two nodes in a graph. Dijkstra's algorithm and A* search are classic examples, crucial for applications like route planning, logistics, and understanding information propagation.
4. Connectivity Analysis: Examining how nodes are connected, identifying components (subgraphs where all nodes are reachable from each other), bridges (edges whose removal increases the number of connected components), and articulation points (nodes whose removal increases the number of connected components).

Challenges in Graph Analysis

Despite their power, graph structures and their analysis present unique challenges. Scalability is a major concern; real-world graphs can contain billions of nodes and trillions of edges, making computation-intensive algorithms prohibitive without distributed computing solutions. Visualization of large, complex graphs can be overwhelming and difficult to interpret, often requiring sophisticated layout algorithms and interactive tools. Dynamic graphs, where nodes and edges appear and disappear over time, add another layer of complexity, demanding methods that can capture temporal evolution. Furthermore, the construction of meaningful graphs from raw, unstructured data often requires significant feature engineering and domain expertise.

The critical insight here is that while graphs excel at showing how things are connected, they often rely on pre-defined relationships or struggle to infer latent similarities that don't manifest as direct links. This is precisely where clustering can offer a valuable antecedent or complementary step. By first grouping similar entities through clustering, the resulting clusters can then be treated as "super-nodes" in a higher-level graph, simplifying complexity and allowing graph analysis to focus on relationships between these learned groups, or conversely, graph properties can enrich the definition of similarity for more effective clustering.

The Synergy: Cluster-Graph Hybrid Models

The true revolutionary potential in data analysis emerges when we move beyond the isolated application of clustering and graph theory, and instead, strategically integrate them into a Cluster-Graph Hybrid model. This synergy allows us to harness the strengths of both paradigms, compensating for their individual weaknesses and unlocking a deeper, more contextualized understanding of data. The hybrid approach is not a monolithic method but rather a spectrum of integration strategies, each designed to address specific analytical challenges by leveraging similarity and connectivity in concert.

The core idea is to establish a dynamic interplay: clustering can inform graph construction or analysis, and conversely, graph properties can enhance the effectiveness of clustering. This iterative or sequential process allows for a mutual refinement of insights, leading to more robust and meaningful discoveries than either method could achieve alone.

Strategies for Integration: A Spectrum of Hybridization

The ways in which clustering and graph analysis can be combined are diverse, reflecting the complexity of real-world data and analytical goals:

1. Graph-Enhanced Clustering: In this approach, graph properties are directly utilized to improve the quality and relevance of clustering.
   • Similarity Graph Construction: Often, the first step in graph-enhanced clustering is to construct a similarity graph where data points are nodes, and edge weights represent their similarity (e.g., using k-nearest neighbors to form edges, or a radial basis function kernel for edge weights). This graph itself encodes the local structure of the data.
   • Spectral Clustering: As previously discussed, spectral clustering is a prime example. It transforms the clustering problem into a graph partitioning problem, using the eigenvectors of the graph Laplacian to project data into a lower-dimensional space where clusters become more linearly separable. This allows for the discovery of non-convex, arbitrarily shaped clusters.
   • Clustering with Graph Regularization: Some clustering algorithms can be modified to incorporate graph-based regularization terms in their objective functions. For instance, in semi-supervised clustering, known labels for a few nodes can propagate through the graph to help cluster unlabeled nodes, ensuring that connected nodes are more likely to be in the same cluster. This ensures that the clusters respect the underlying network structure.
   • Community Detection as Clustering: In many contexts, particularly in network science, community detection algorithms (e.g., Louvain, Leiden) are effectively a form of clustering on graph data. They group nodes into communities based on the density of internal connections versus external connections, yielding structurally coherent clusters.
2. Clustering-Enhanced Graphs: Here, the results of clustering are used to simplify, enrich, or analyze graphs more effectively.
   • Abstracting Graphs with Clusters: For very large and dense graphs, individual node-level analysis can be computationally prohibitive and yield too much granular detail. Clustering can group similar nodes into "super-nodes" or "meta-nodes." A new, smaller graph can then be constructed where each super-node represents a cluster, and edges between super-nodes indicate connections between their constituent members. This "coarse-graining" or "graph summarization" simplifies the graph, making higher-level patterns and relationships between groups more discernible. For instance, after clustering customers, a graph connecting these customer segments can reveal inter-segment influence.
   • Enriching Node Attributes with Cluster Membership: Cluster assignments can be added as new attributes to the nodes in an existing graph. This enrichment allows graph analytics to be performed on heterogeneous data, where node properties (e.g., demographic data for people, functional roles for proteins) can now include their assigned cluster. This can be particularly useful for identifying relationships between nodes that share certain cluster characteristics.
   • Analyzing Inter-Cluster Connectivity: Once clusters are formed, the focus shifts to understanding how these clusters are connected within the broader network. Are certain clusters highly isolated? Do others act as bridges between disparate parts of the network? This reveals macro-level structural insights that simple node-level graph analysis might miss.
3. Iterative and Feedback Loops: The most sophisticated hybrid models involve iterative processes where clustering and graph analysis continuously inform and refine each other.
   • Initial clustering might reveal some structure, which is then used to refine a similarity graph. This refined graph, in turn, can lead to a more accurate clustering, and so on.
   • For example, in entity resolution, clustering might group records that are likely the same entity. A graph could then be built where nodes are potential entities, and edges represent evidence of coreference. Graph-based inference (e.g., finding connected components) can further merge or split clusters, with the updated clusters feeding back into the similarity calculation.

Architectural Considerations for Hybrid Systems

Implementing Cluster-Graph Hybrid models requires careful architectural design, especially when dealing with large-scale, complex data. Key considerations include: * Data Representation: How to seamlessly transform data between tabular formats (for clustering) and graph formats (for graph analysis). * Scalability: Utilizing distributed computing frameworks (e.g., Apache Spark's GraphX) or specialized graph databases (e.g., Neo4j, Amazon Neptune) that can handle billions of nodes and edges. * Workflow Orchestration: Managing the sequence of clustering and graph analysis steps, including data loading, algorithm execution, result storage, and visualization.

Introducing Model Context Protocol (MCP) / mcp: The Glue for Hybrid Models

In the intricate dance of a Cluster-Graph Hybrid system, where multiple analytical models (clustering algorithms, graph algorithms, perhaps even machine learning classifiers) interact and exchange information, a robust Model Context Protocol (MCP) becomes absolutely essential. Think of the mcp as the communication standard and data governance framework that ensures seamless, consistent, and context-aware interaction between the different components of the hybrid system.

The Model Context Protocol defines: 1. Data Exchange Formats: Standardized schemas for how clustering outputs (e.g., cluster assignments, centroid properties) are ingested by graph construction processes, or how graph features (e.g., centrality scores, community labels) are provided as input for refining clustering. This ensures that information passed between models is correctly interpreted and utilized. 2. Contextual Preservation: As data flows from one model to another, its underlying context must be preserved. For example, if a graph component identifies a critical "bridge node," the mcp ensures that this contextual information (e.g., why it's a bridge, which clusters it connects) is available if that node later becomes part of a cluster analysis. This avoids loss of crucial metadata and analytical provenance. 3. Versioning and Provenance: In complex analytical pipelines, especially those that are iterative, tracking the origin and transformation of data and model outputs is paramount. The Model Context Protocol dictates how metadata about model versions, input datasets, and transformation steps are recorded, providing transparency and reproducibility for the entire analysis. 4. Error Handling and State Management: The mcp can also include specifications for how errors or inconsistencies are handled when data is exchanged between models, ensuring the robustness and reliability of the hybrid system. It also dictates how the "state" of the analysis (e.g., current cluster assignments, graph structure) is maintained across iterative steps. 5. Interoperability: By standardizing interfaces and data formats, the Model Context Protocol facilitates the integration of diverse tools and algorithms within the hybrid framework. This allows researchers and developers to mix and match state-of-the-art clustering algorithms with specialized graph analysis tools, knowing they can communicate effectively.

Without a well-defined mcp, a Cluster-Graph Hybrid system risks becoming a chaotic collection of loosely coupled scripts, prone to data misalignment, contextual ambiguities, and difficult debugging. The Model Context Protocol acts as the crucial architectural backbone, ensuring that the powerful synergy between clustering and graph analysis is not undermined by communication breakdowns.

Real-world Applications and Use Cases

The versatility of Cluster-Graph Hybrid models makes them applicable across a wide spectrum of domains, leading to profound insights:

1. Social Network Analysis:
   • Problem: Identifying influential individuals and cohesive communities, and understanding information flow.
   • Hybrid Approach: First, clustering individuals based on attributes (demographics, interests, activity patterns) to identify latent user segments. Then, build a graph where nodes are individuals (with cluster labels as attributes) and edges represent social connections. Apply community detection on the graph, potentially using cluster labels to guide or validate communities. Graph centrality measures can then identify influential users within specific clusters or bridges between different clusters, revealing opinion leaders or gatekeepers. This combined view provides a much richer understanding than just looking at connections or attributes separately.
2. Bioinformatics and Drug Discovery:
   • Problem: Understanding protein-protein interaction (PPI) networks, identifying disease pathways, and finding drug targets.
   • Hybrid Approach: Cluster proteins based on their functional domains, gene expression profiles, or structural similarities. Then, construct a PPI graph where nodes are proteins (with cluster assignments) and edges represent known interactions. Community detection on this graph can reveal functional modules or disease pathways. Analyzing the connectivity between different protein clusters (e.g., an enzyme cluster interacting heavily with a signaling pathway cluster) can pinpoint critical points for therapeutic intervention. The Model Context Protocol here would be vital for managing the flow of protein features, interaction data, and cluster assignments across various bioinformatic tools.
3. Fraud Detection and Cybersecurity:
   • Problem: Identifying suspicious activities that might be hidden within normal patterns.
   • Hybrid Approach: Cluster transactions or user accounts based on behavioral patterns, transaction amounts, frequency, or geographic locations. Anomalous clusters (e.g., a cluster of accounts with unusual transaction volumes) can be flagged. Then, build a graph where nodes are accounts/transactions (with cluster labels) and edges represent their relationships (e.g., shared IP addresses, fund transfers, common beneficiaries). Graph analysis can reveal highly interconnected "fraud rings" or "attack campaigns" that might span multiple seemingly disparate clusters, where individual suspicious activities merge into a larger illicit network. Betweenness centrality could highlight accounts acting as central conduits in fraud networks.
4. Recommendation Systems:
   • Problem: Suggesting relevant items (products, movies, content) to users.
   • Hybrid Approach: Cluster users based on their historical preferences, demographics, or browsing behavior. Also, cluster items based on their features (genre, tags, actors). Then, build a bipartite graph connecting users to items they have interacted with. Additionally, a graph representing inter-item similarity or inter-user similarity (derived from clustering) can be created. The hybrid model can then leverage both the explicit user-item interactions and the latent similarities from clustering to provide more accurate and diverse recommendations, potentially suggesting items popular within a user's cluster or items connected to previously liked items in a personalized knowledge graph.
5. Urban Planning and Transportation:
   • Problem: Optimizing public transport routes, identifying areas with similar demographic profiles, or understanding traffic flow.
   • Hybrid Approach: Cluster urban areas (e.g., census tracts) based on socio-economic indicators, population density, or infrastructure. Then, construct a transportation network graph where nodes are intersections/stations (with cluster context of the surrounding area) and edges are roads/routes (with traffic data as weights). Graph algorithms can identify bottlenecks, optimal routes considering both travel time and the characteristics of the areas traversed, or how different urban clusters are connected by the transportation network.

These examples vividly illustrate how the Cluster-Graph Hybrid approach, meticulously managed by a robust Model Context Protocol, moves beyond fragmented insights to deliver a comprehensive understanding of complex systems.

Integration Strategy	Description	Primary Goal	Example Use Case
Graph-Enhanced Clustering	Uses graph-derived information (e.g., connectivity, proximity, Laplacian matrix) to improve or perform clustering.	Discover natural groupings that respect underlying network structure.	Spectral Clustering for non-convex shapes; Community Detection on social networks.
Clustering-Enhanced Graphs	Uses cluster assignments to simplify, enrich, or add context to graph nodes and edges.	Simplify large graphs, add semantic context to nodes, analyze inter-cluster relationships.	Coarse-graining a large graph into "super-nodes" (clusters); Attaching demographic clusters to urban area nodes.
Iterative/Feedback Loops	Clustering and graph analysis continuously inform and refine each other in a multi-step process.	Achieve mutual refinement of insights, handle complex dependencies.	Entity Resolution with graph-based merge/split; Anomaly detection with iterative pattern refinement.
Integrated Feature Spaces	Directly combine features from both domains (e.g., node attributes + graph embeddings) for a unified model.	Create a holistic representation for downstream machine learning tasks.	Combining user demographic clusters, interaction graph embeddings for personalized recommendations.

APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇

Implementing and Deploying Hybrid Models

The journey from conceptualizing a Cluster-Graph Hybrid model to its robust implementation and scalable deployment involves navigating a landscape of technological choices and overcoming significant engineering challenges. The effectiveness of these sophisticated analytical pipelines hinges not only on the theoretical soundness of the models but critically on the underlying infrastructure and the mechanisms that manage their interaction.

The Technological Stack: Tools for Hybrid Analytics

Building a Cluster-Graph Hybrid system typically requires a combination of specialized libraries, frameworks, and databases:

1. For Clustering:
   • Python Libraries: scikit-learn is the de-facto standard for classical machine learning, offering implementations of K-means, DBSCAN, hierarchical clustering, and spectral clustering. hdbscan is an excellent choice for density-based clustering.
   • R Packages: cluster, factoextra, dbscan provide similar functionalities in the R ecosystem.
   • Distributed Frameworks: For massive datasets, clustering algorithms can be parallelized using Apache Spark (e.g., MLlib for K-means) or custom implementations on distributed computing clusters.
2. For Graph Analysis:
   • Graph Databases: These are purpose-built databases optimized for storing and querying highly interconnected data.
     • Neo4j: A leading native graph database, offering high performance for complex graph traversals and pattern matching with its Cypher query language. It's excellent for applications requiring deep link analysis.
     • Amazon Neptune: A fully managed graph database service that supports popular graph models (Property Graph and RDF) and their respective query languages (Gremlin and SPARQL).
     • ArangoDB: A multi-model database that supports graphs, documents, and key-value stores.
   • Graph Processing Frameworks: For analytical tasks on large graphs, these frameworks enable distributed graph computations.
     • Apache Spark GraphX: A component of Apache Spark for graph-parallel computation, allowing users to build and transform graphs, and implement various graph algorithms (PageRank, Connected Components, SVD, etc.) at scale.
     • Apache Flink Gelly: Another graph processing library integrated with Apache Flink.
   • Python Libraries: NetworkX is an indispensable library for creating, manipulating, and studying the structure, dynamics, and functions of complex networks in Python. igraph offers similar capabilities with a focus on performance.
3. Data Integration and Orchestration:
   • Data Lakes/Warehouses: Storing raw and processed data (e.g., Apache Hadoop HDFS, AWS S3, Snowflake) that feeds into the hybrid pipeline.
   • ETL/ELT Tools: Tools like Apache NiFi, Airflow, or custom scripts for extracting, transforming, and loading data between different components.
   • Workflow Management: Orchestrators like Apache Airflow or Kubeflow Pipelines for managing the complex dependencies and execution order of clustering and graph analysis tasks.

Challenges in Deployment

Deploying Cluster-Graph Hybrid models in production environments introduces several challenges:

• Scalability: Handling ever-growing datasets and graph sizes requires highly optimized algorithms and distributed architectures. Simply running local libraries on large datasets is often insufficient.
• Real-time Processing: Many applications demand near real-time insights (e.g., fraud detection). This necessitates streaming data pipelines and low-latency graph query capabilities.
• Data Integration: Merging diverse data sources, cleaning, and transforming them into a consistent format suitable for both clustering and graph construction is a non-trivial task.
• Interpretability: Understanding why a particular cluster was formed or why certain relationships exist in a complex graph can be challenging, especially in deep learning-based hybrid models. Explainable AI techniques are becoming increasingly important.
• Maintenance and Monitoring: Production systems require continuous monitoring of data quality, model performance, and infrastructure health, along with processes for model retraining and updates.

The Role of LLMs and LLM Gateways: Bridging Insights with Natural Language

As Cluster-Graph Hybrid models generate increasingly complex insights, often expressed in numerical scores, cluster labels, or intricate graph structures, the ability to interpret, synthesize, and interact with these insights in a human-understandable way becomes paramount. This is where Large Language Models (LLMs) enter the picture, offering a powerful avenue for natural language interpretation, generation, and interaction.

LLMs can play several transformative roles: * Interpretation and Summarization: An LLM can be prompted to interpret the characteristics of a newly discovered cluster (e.g., "describe the common attributes of customers in cluster 3 based on these features") or summarize the structural properties of a specific graph community (e.g., "explain why these genes form a tightly connected module and their potential function"). * Query Generation and Refinement: Instead of writing complex graph queries or configuring clustering parameters, users could describe their analytical goals in natural language, and an LLM could translate these into executable queries or model configurations. * Narrative Generation: LLMs can generate comprehensive reports or narratives from the combined outputs of clustering and graph analysis, making complex findings accessible to non-technical stakeholders. For example, generating a story about a fraud incident by linking suspicious transactions (from clusters) with their network of collaborators (from the graph). * Contextual Understanding: LLMs, especially when fine-tuned on domain-specific knowledge, can help enrich the Model Context Protocol by providing semantic meaning to data elements or relationships, ensuring that the context is not just syntactically correct but also semantically understood across different models.

However, integrating LLMs into complex analytical pipelines, especially those dealing with sensitive or high-volume data, introduces its own set of challenges: managing multiple LLM providers, ensuring data privacy, controlling costs, and maintaining consistent API access. This is precisely where an LLM Gateway becomes not just beneficial, but indispensable.

An LLM Gateway acts as a crucial abstraction layer between your hybrid analytical system and the diverse LLMs (e.g., OpenAI, Anthropic, Google Gemini, open-source models) it might leverage. When you're leveraging multiple AI models, including LLMs to process the outputs or guide the inputs of your Cluster-Graph Hybrid system, an LLM Gateway like APIPark provides a unified interface for managing these diverse AI services. It ensures consistent API formats across different providers, handles authentication, monitors usage, implements rate limiting, and enables seamless integration, drastically simplifying the operational overhead.

Specifically, an LLM Gateway contributes to the success of Cluster-Graph Hybrid systems in several ways: * Unified API Format: It normalizes the request and response formats from various LLM providers, meaning your hybrid system doesn't need to be rewritten every time you switch or add a new LLM model. This consistency aligns perfectly with the principles of a robust Model Context Protocol, ensuring that contextual information flows smoothly to and from the LLM. * Authentication and Access Control: Centralizes the management of API keys and access permissions for different LLMs, enhancing security and simplifying administrative tasks. * Cost Management and Tracking: Provides detailed logging and analytics on LLM usage, enabling enterprises to track costs, optimize spending, and attribute usage to specific projects or teams within the hybrid analysis pipeline. * Load Balancing and Fallback: Can distribute requests across multiple LLM instances or providers, ensuring high availability and performance. If one LLM service goes down or becomes overloaded, the gateway can automatically route requests to another. * Prompt Management and Versioning: Facilitates the management of prompts used for LLM interactions. This is critical for ensuring that the LLM consistently interprets cluster characteristics or generates narratives based on graph patterns, and allows for versioning of prompts as analytical goals evolve. * Context Management and State Preservation: While the Model Context Protocol defines how context should be managed at an architectural level, an LLM Gateway can implement parts of this protocol by ensuring that session-specific context or conversation history is correctly passed to the LLM, enabling more coherent and relevant responses within the hybrid analytical workflow. * Performance and Scalability: Commercial-grade gateways are designed for high throughput and low latency, capable of handling the demands of large-scale analytical systems that frequently query LLMs. APIPark, for example, boasts performance rivaling Nginx, achieving over 20,000 TPS with an 8-core CPU and 8GB memory, and supporting cluster deployment for massive traffic. This level of performance is critical when LLMs are integrated into real-time analytical loops or serve many concurrent users.

By abstracting away the complexities of interacting with various LLMs and other AI services, an LLM Gateway allows developers and data scientists to focus on the core task of extracting insights from their Cluster-Graph Hybrid models, rather than getting bogged down in infrastructure management. This seamless integration of AI capabilities, facilitated by robust gateways like APIPark, marks a significant step forward in making advanced analytical insights more accessible and actionable.

Future Directions and Advanced Concepts

The landscape of Cluster-Graph Hybrid models is continuously evolving, driven by advancements in data science, artificial intelligence, and computing infrastructure. Several exciting frontiers promise to further amplify the power and applicability of these hybrid approaches.

One significant area of development is Dynamic Graphs and Temporal Clustering. Most traditional graph and clustering algorithms assume static data, but real-world systems are inherently dynamic. Networks evolve, relationships appear and disappear, and data points change their characteristics over time. Future hybrid models will increasingly focus on algorithms that can capture these temporal dynamics. This involves not only detecting evolving communities in dynamic graphs but also applying temporal clustering techniques that group data points based on their changing behavior over time. Integrating these temporal insights into a hybrid framework will enable the analysis of dynamic social networks, evolving biological pathways, or real-time fraud patterns with unprecedented precision. The Model Context Protocol will need to expand to explicitly include temporal metadata and handle time-series data streams effectively across models.

Another rapidly expanding domain is Deep Learning on Graphs (Graph Neural Networks - GNNs). GNNs are a class of neural networks designed to operate directly on graph-structured data, capable of learning powerful node, edge, or graph-level representations. By integrating GNNs, Cluster-Graph Hybrid models can move beyond traditional feature engineering and similarity metrics, leveraging the capacity of deep learning to automatically learn complex patterns and relationships. For instance, GNNs could learn node embeddings that inherently capture both attribute similarity and network connectivity, which can then be directly fed into a clustering algorithm. Conversely, initial clustering might be used to define "super-nodes" for a hierarchical GNN architecture, making it more scalable. The combination of GNNs with classical clustering techniques offers a potent avenue for discovering highly nuanced and multi-modal insights.

Explainable AI (XAI) for Hybrid Models is also gaining critical importance. As these models grow in complexity, understanding why a particular insight was generated becomes as crucial as the insight itself, especially in high-stakes applications like healthcare or finance. Developing XAI techniques specifically for Cluster-Graph Hybrid models will involve methods to interpret the contributions of both clustering and graph components to the final outcome. This might include techniques to visualize the decision boundaries of clusters in the context of graph structures, or to highlight the most influential nodes and edges that led to a specific anomaly detection. A comprehensive Model Context Protocol would be instrumental here, storing and exposing the lineage of decisions and transformations within the hybrid pipeline to aid interpretability.

Finally, Ethical Considerations are becoming increasingly central to the deployment of any advanced analytical system. Cluster-Graph Hybrid models, especially when applied to sensitive data (e.g., individual behavior, social demographics), carry the risk of perpetuating biases present in the data, or even creating new forms of discrimination through algorithmic decisions. Future developments must incorporate fairness metrics, bias detection, and ethical guidelines into the design and evaluation of these models. This includes ensuring transparency in data collection, model training, and algorithmic output, as well as developing mechanisms for redress. The LLM Gateway, if used for explaining insights, must also be designed to communicate potential biases or uncertainties in the model's outputs responsibly.

These future directions underscore the vibrant and evolving nature of Cluster-Graph Hybrid analytics. As data continues to grow in complexity and volume, the need for sophisticated, integrated approaches that can reveal deep, contextual insights will only intensify, pushing the boundaries of what is possible in data science.

Conclusion

The journey through the intricate world of Cluster-Graph Hybrid models reveals a profound truth: the future of data analytics lies in the intelligent integration of diverse methodological paradigms. No single technique, whether it be the meticulous grouping offered by clustering or the relational insights provided by graph theory, can fully encapsulate the multi-faceted complexity of modern datasets. It is in their powerful synergy that we unlock unprecedented levels of understanding, transforming raw data into actionable wisdom.

From elucidating hidden communities in social networks to pinpointing critical disease pathways in bioinformatics, and from detecting sophisticated fraud rings to enhancing personalized recommendation systems, the Cluster-Graph Hybrid approach demonstrates its immense versatility and analytical superiority. By allowing data to be viewed simultaneously through the lens of similarity and connectivity, these models empower us to see not just the individual components, but the intricate web of relationships that defines the entire system.

Crucial to the successful implementation and scalable deployment of these sophisticated hybrid systems are foundational architectural elements. The Model Context Protocol (MCP) emerges as an indispensable framework, serving as the connective tissue that ensures seamless, consistent, and context-aware communication between disparate analytical components. It standardizes data exchange, preserves contextual meaning, and provides the necessary scaffolding for robust, reproducible insights. Equally vital, particularly in an era increasingly powered by artificial intelligence, is the role of an LLM Gateway. By providing a unified, performant, and secure interface for interacting with various Large Language Models, solutions like APIPark abstract away the complexities of AI integration. This allows organizations to leverage LLMs for interpreting, synthesizing, and interacting with the rich insights generated by Cluster-Graph Hybrid models, without being burdened by the operational overhead of managing diverse AI services.

As we look ahead, the continuous evolution of these hybrid models, fueled by advancements in dynamic graph analysis, deep learning on graphs, and explainable AI, promises to further revolutionize our capacity to derive intelligence from data. The challenges of scalability, real-time processing, and ethical deployment remain, yet with robust protocols and intelligent gateways in place, the path forward is clear. The Cluster-Graph Hybrid paradigm, augmented by an intelligent ecosystem, is not merely an analytical technique; it is a strategic imperative for any entity seeking to thrive in the data-driven future. It empowers us to move beyond superficial observations, diving deep into the interconnected fabric of information to unlock truly transformative insights.

---

5 FAQs about Cluster-Graph Hybrid Models

1. What is a Cluster-Graph Hybrid Model and why is it superior to using clustering or graph analysis alone? A Cluster-Graph Hybrid Model is an advanced analytical approach that integrates the principles of cluster analysis with graph theory. It leverages clustering to identify inherent groupings or similarities within data, and graph analysis to uncover explicit relationships and interactions between data points or even between the clusters themselves. This hybrid approach is superior because it overcomes the individual limitations of each method: clustering might miss relational context, while graph analysis might struggle to infer latent similarities. By combining them, the model gains a more holistic, contextualized, and robust understanding of complex data, revealing insights that neither method could fully achieve on its own.

2. How does the Model Context Protocol (MCP) contribute to the effectiveness of a Cluster-Graph Hybrid system? The Model Context Protocol (MCP), or mcp, acts as the crucial communication and data governance standard within a Cluster-Graph Hybrid system. It defines standardized ways for different analytical components (e.g., clustering algorithms, graph databases, LLMs) to exchange data and information, ensuring that insights derived from one model are correctly interpreted and utilized by another. MCP is vital for preserving contextual information, maintaining data integrity, managing versions, handling errors, and ensuring the overall interoperability and reproducibility of the complex analytical pipeline. Without a robust MCP, the hybrid system would risk data misalignment and communication breakdowns, diminishing its effectiveness.

3. In what real-world scenarios can Cluster-Graph Hybrid models be most effectively applied? Cluster-Graph Hybrid models are highly effective in scenarios where both inherent groupings and explicit relationships are critical for understanding complex systems. Key applications include: * Social Network Analysis: Identifying influential communities and individuals by clustering users by attributes and analyzing their social connections. * Bioinformatics: Uncovering functional protein modules and disease pathways by clustering proteins by function and analyzing their interaction networks. * Fraud Detection: Detecting sophisticated fraud rings by clustering suspicious transactions and mapping their network of connections. * Recommendation Systems: Providing personalized recommendations by clustering users/items and leveraging their interaction graphs. * Urban Planning: Optimizing transportation and resource allocation by clustering urban areas by demographics and analyzing infrastructure connectivity.

4. What role does an LLM Gateway play in implementing and deploying these hybrid models? An LLM Gateway plays an indispensable role in integrating Large Language Models (LLMs) into Cluster-Graph Hybrid systems, especially in production environments. It acts as an abstraction layer, providing a unified interface for interacting with various LLM providers (e.g., OpenAI, Anthropic). This simplifies management of diverse AI services, ensures consistent API formats, centralizes authentication and access control, tracks costs, and enables features like load balancing and prompt versioning. For example, APIPark provides such a gateway, allowing developers to seamlessly use LLMs to interpret cluster characteristics, generate insights from graph patterns, or interact with the analytical system in natural language, without the operational complexities of direct LLM integration.

5. What are some of the key challenges in deploying Cluster-Graph Hybrid models and how are they being addressed? Deploying Cluster-Graph Hybrid models faces several key challenges: * Scalability: Handling vast datasets and graphs requires distributed computing frameworks (e.g., Apache Spark GraphX) and specialized graph databases (e.g., Neo4j). * Real-time Processing: Many applications demand low-latency insights, necessitating streaming data pipelines and high-performance graph query capabilities. * Data Integration: Merging and transforming diverse data sources into consistent formats for both clustering and graph analysis can be complex, often addressed with robust ETL pipelines and workflow orchestrators. * Interpretability: Understanding the 'why' behind complex insights requires developing Explainable AI (XAI) techniques tailored for hybrid models. * Ethical Considerations: Ensuring fairness and preventing bias requires incorporating ethical guidelines and bias detection mechanisms into model design and evaluation. These challenges are being addressed through continuous advancements in distributed computing, specialized graph technologies, AI/ML engineering best practices, and the growing field of Responsible AI.

🚀You can securely and efficiently call the OpenAI API on APIPark in just two steps:

Step 1: Deploy the APIPark AI gateway in 5 minutes.

APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.

curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh

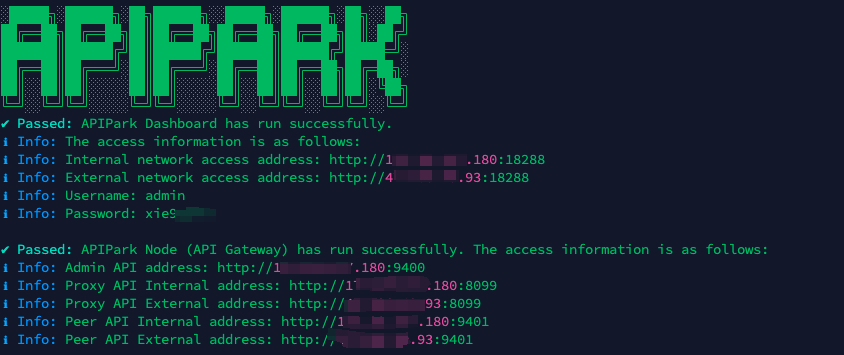
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.

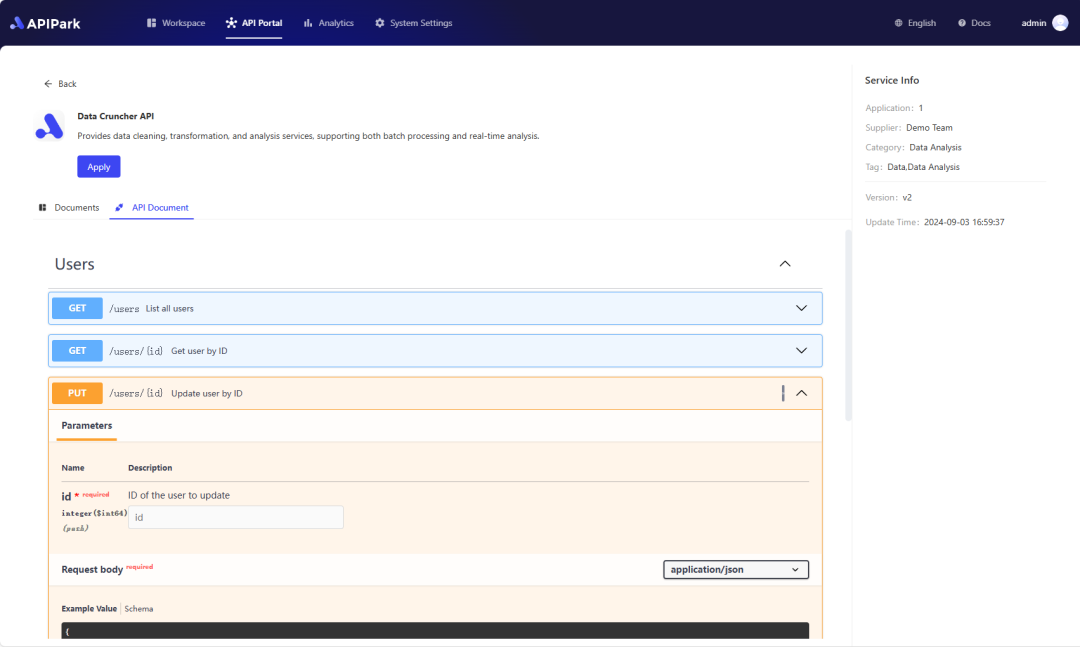
Step 2: Call the OpenAI API.