Understanding 3.4 as a Root in Mathematical Concepts

Mathematics is a vast field that encompasses various ideas, theories, and practices. Among the many concepts studied in mathematics, the notion of roots stands out due to its fundamental significance in various applications, from solving equations to understanding geometric relationships. In this article, we will delve deeply into understanding the mathematical expression “3.4 as a root” while simultaneously exploring how this concept links to broader themes such as API Gateway, OpenAPI, and API Governance through the lens of modern technology, particularly in relation to the functionalities provided by platforms like APIPark.

What are Roots?

At its core, a root is a value that, when substituted for the variable in an equation, yields zero. It reflects the points at which graphical representations touch or cross the x-axis. For instance, the expression (x^2 - 3.4 = 0) reveals that (x = \sqrt{3.4}) is a root of the quadratic equation. Roots do not merely represent numerical values; they also serve as seconds to explore the solution to polynomial equations.

To better comprehend the concept of roots, let’s represent roots in tabular format where we examine some roots from various polynomial equations.

Polynomial Equation	Degree	Roots
(x^2 - 4 = 0)	2	(x = 2, -2)
(x^3 - 6x + 8 = 0)	3	Approximately (x = -2, 2, \approx 1)
(x^4 - 3.4x^2 + 2 = 0)	4	Complex roots
(x^5 - 3.4 = 0)	5	Fifth roots of (3.4)

The table above illustrates the roots of different polynomial equations and their importance in mathematical problem-solving. A polynomial degree corresponds with possible roots, and understanding them equips one to tackle complex mathematical challenges.

Exploring Decimal Roots: The Case of 3.4

To grasp "3.4 as a root", let’s first express it in different contexts. The fact that values can represent more than mere integers expands the utility of roots. A decimal root, particularly ( \sqrt{3.4} ), indicates that we are exploring roots beyond simple whole numbers, which often leads to non-integer outcomes.

Calculation of the Decimal Root

The calculation of ( \sqrt{3.4} ) gives us an approximate value of 1.843. This means that if we square 1.843, we obtain back 3.4, assuring its validity as a root in mathematical practice:

[ (1.843)^2 \approx 3.4 ]

Implications of Decimal Roots in Mathematics

Understanding and utilizing decimal roots expands our grasp of functions and their limits. They enable mathematicians and scientists to model real-world scenarios, such as measuring distances in physics or predictive analytics in data science.

In the modern digital era, such modeling is often facilitated through APIs, which specific platforms like APIPark efficiently manage. These platforms take advantage of mathematical principles, including roots, to provide services that require precise calculations and data manipulations. For instance, the effective governance and management of AI models through robust API frameworks can enhance computational efficiency.

APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇

The Intersection of Mathematical Concepts and Technology

In our digital age, the interplay between mathematical principles and technology becomes increasingly significant. Every mathematical concept, including roots, directly impacts various tech domains, such as API development and management.

API Gateways and Mathematical Frameworks

An API gateway acts as a single entry point for several APIs, streamlining the processes of request routing, composition, and protocol translation. Just as roots represent the foundation of polynomial equations, API gateways serve as the groundwork for API-based architecture. They allow developers to manage numerous API calls with a uniform access point.

One of the valuable platforms in this field is APIPark, which offers open-source API management and AI gateway services. With its ability to integrate several AI models and facilitate seamless API governance, APIPark symbolizes the critical relationship between mathematical concepts and practical technology applications.

Understanding OpenAPI

OpenAPI is another essential area where mathematical foundations play a considerable role. It defines a standard, language-agnostic interface to RESTful APIs. This standardization allows developers to understand the functionalities provided by an API swiftly.

Mathematics governs the way APIs are structured, particularly in how they handle data. The systematic organization of data flows, character validations, and other functional attributes often rely on underlying mathematical principles akin to those found within polynomial equations.

Feature	Description
API Standardization	Ensures consistent design and usability
Version Control	Manages how updates affect existing functionality
Reliability and Security	Mathematical standards ensure data integrity
Ease of Integration	Frictionless onboarding of diverse services

This table illustrates how API functionalities, much like mathematical operations, rely on well-defined principles and structures.

API Governance and Data Optimization

API governance represents critical importance in maintaining the integrity and efficiency of APIs. It assigns rules regarding API access, usage, performance monitoring, and other operational parameters. In this context, mathematics again provides the backbone for these systems—mathematical functions are used alongside algorithms to measure API performance, analyze traffic, and optimize resource utilization.

As highlighted earlier, platforms like APIPark facilitate effective API governance by offering essential features that regulate the lifecycle of APIs. Interpreting data patterns through mathematical models allows enterprises to foresee potential issues before they manifest—ensuring robustness and reliability.

Mathematical Modeling and Predictive Analysis

Employing mathematical concepts, particularly roots, as a basis for modeling allows us to create predictive analytics that address real-world scenarios. For instance, when solving physical equations that express forces or motions, understanding roots leads us to formulate accurate predictive models.

Unquestionably, if a function has a root, it may indicate equilibrium or stability in a system. For instance, in the technological domain, especially when dealing with API integrations, knowing the roots allows developers to predict how changes might impact system functionality.

The Role of APIPark in Predictive Analytics

In this light, an API management platform like APIPark encapsulates mathematical precision through its analytical features. By analyzing historical data, APIPark can identify trends and potential areas for optimization. In turn, users can fine-tune their API services, ensuring peak performance.

Predictive Modeling Example

To illustrate how mathematical modeling is intertwined with API functionalities, consider creating an API service that forecasts sales based on historical data. The underlying mathematical model would typically involve:

1. Data Collection (historical sales data)
2. Function Representation (approximately obtaining the root of polynomial equations)
3. Predictive Output (future sales expectations)

Through APIPark’s capabilities, this entire process can be streamlined and managed effortlessly.

Conclusion

Understanding “3.4 as a root” brings mathematical concepts to life, reiterating their significance in contemporary technology. The principles governing roots, especially decimal roots, seamlessly translate into the domain of API development and management.

APIs stand as a vital interface within technological ecosystems, governed by mathematical structures that ensure their efficacy. With platforms like APIPark, not only can developers manage APIs effectively, but they also leverage powerful mathematical analyses to enhance predictive modeling and optimization processes.

In conclusion, the fusion of mathematical concepts and modern technology proves integral for delivering robust software solutions, guiding developers, and empowering enterprises towards achieving their operational goals.

FAQs

1. What is the mathematical definition of a root? A root is a value that satisfies an equation such that it makes the equation equal to zero.
2. How is the concept of roots applied in programming? In programming, roots are often utilized in algorithms where solving mathematical equations or input processing is required, particularly in API data manipulations.
3. What are API Gateways? API Gateways are server components that act as a single entry point for multiple APIs, managing requests, traffic, security, and protocols.
4. What is the relevance of OpenAPI in API development? OpenAPI defines a language-agnostic specification that standardizes the development and documentation of RESTful APIs, enabling better collaboration and comprehension.
5. How does APIPark integrate mathematical principles in its functionalities? APIPark leverages mathematical models to optimize API performance, predict analytics, and enhance data management through governing rules and standards.

🚀You can securely and efficiently call the OpenAI API on APIPark in just two steps:

Step 1: Deploy the APIPark AI gateway in 5 minutes.

APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.

curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh

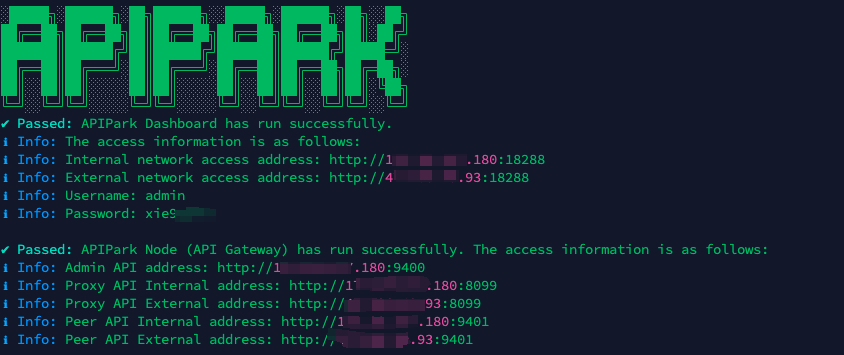
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.

Step 2: Call the OpenAI API.

Learn more