Understanding 3.4 as a Root: Concepts and Applications

In mathematics, roots play a crucial role in understanding the properties of numbers and their relationships. Among these roots, the value 3.4 is particularly interesting when dissected in both theoretical and practical applications. In this article, we will delve into the concept of 3.4 as a root, explore its mathematical implications, and examine various applications in the realm of APIs, particularly with the utilization of OpenAPI specifications and API gateways such as APIPark.

Table of Contents

1. Introduction to Roots
2. Understanding 3.4 as a Root
3. Applications in Algorithms
4. APIs and Their Role
5. OpenAPI Specifications
6. API Gateways: Streamlining Communication
7. The Role of APIPark in API Management
8. Conclusion
9. Frequently Asked Questions (FAQ)

Introduction to Roots

In mathematics, a root is a value that, when substituted for a variable, satisfies an equation. Roots can be classified into different types based on the power to which a number is raised. For example, the second root corresponds to the square root, while the third root is known as the cube root. The concept of roots is fundamental in algebra and is widely applied in various branches of mathematics, engineering, and computer science.

Basic Concepts of Roots

• Square Roots: If (x^2 = a), then (x) is the square root of (a).
• Cube Roots: If (x^3 = a), then (x) is the cube root of (a).
• Higher Roots: This concept can be extended to any positive integer (n), where (x^n = a).

The Importance of Roots

Roots help in simplifying complex equations and provide insight into the behavior of functions. They play a pivotal role in calculus, optimization problems, and numerical analysis. In the context of data science and machine learning, understanding these mathematical principles can aid in achieving better models and predictions.

Understanding 3.4 as a Root

To understand 3.4 in the context of roots, let’s consider various scenarios. The value of 3.4 can be approached as a potential root of several polynomial equations. Evaluating this concept mathematically requires further exploration of its nature and properties.

Mathematical Evaluation

Given an equation of the form: [ x^n = a ] the solution for (x) can be expressed as: [ x = a^{1/n} ] Thus, 3.4 could serve as either a solution to such an equation or as a potential "a" in cases where the polynomial's exponent equates to an integer. This understanding lays the groundwork for applying the concept of roots in practical scenarios.

Finding Polynomial Representations

One interesting aspect of dealing with roots involves polynomial functions. A polynomial can be expressed as: [ f(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0 ] where (c_n, c_{n-1}, \ldots, c_0) are coefficients. If we consider incorporating 3.4 as a root, we look at how polynomials change and behave around this value.

Example Equations

If (3.4) is a root, we can derive from: [ f(3.4) = 0 ] constructing an equation, for example: [ f(x) = (x - 3.4)(x - r_1)(x - r_2) ] where (r_1) and (r_2) are other roots. This polynomial provides a tangible application of roots in mathematics.

Significance in Data Science

In data science, the value of (3.4) could signify a threshold or critical value in algorithms reliant on regression or classification frameworks. Understanding the roots of equations enables data scientists to optimize features and improve model predictions effectively.

Applications in Algorithms

The concept of roots, particularly values like 3.4, finds applications in various algorithmic implementations. Let's examine how roots interact within algorithmic frameworks.

Optimization Algorithms

In optimization problems, the derivatives of functions are utilized to locate minima and maxima. The presence of roots can help in pinpointing critical values where the function's slope becomes zero.

Algorithm Type	Description	Example
Gradient Descent	Finds local minima by iteratively moving towards the steepest descent	Optimizing cost functions in machine learning
Newton's Method	Utilizes root-finding for fast convergence in optimization problems	Solving complex equations with multiple variables

Root-finding Algorithms

This includes algorithms such as the bisection method, Newton-Raphson method, and secant method—all of which are designed to approximate roots of real-valued functions.

1. Bisection Method: It divides an interval in half and selects which half contains the root, iteratively narrowing down to the precise value.
2. Newton-Raphson Method: This is a more sophisticated root-finding method that uses tangents to approximate how to find roots effectively.

Machine Learning Algorithms

In machine learning, especially in areas like regression analysis, the roots of a prediction function signify the points where predictions change dramatically. The accuracy of these predictions can be significantly influenced by understanding where roots lie relative to thresholds.

APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇

APIs and Their Role

The advent of APIs (Application Programming Interfaces) has revolutionized how software components interact. Within systems that employ mathematical functions—such as those involving roots—APIs facilitate data exchange and integrate functionalities across different platforms.

API Functionality

APIs provide a set of protocols for building and integrating application software. They allow different software entities to communicate, simplifying the process of extending or leveraging existing functionalities. Here’s how roots, especially when numerically computed, can interact with APIs:

1. Root Calculation APIS: Libraries can be developed offering endpoint access to functions that compute roots of various mathematical equations.
2. Integration with Front-End Applications: Front-end applications can leverage these APIs to provide real-time calculations, such as finding polynomial roots based on user inputs instantly.

RESTful APIs

RESTful APIs are designed around performance, scalability, and maintenability—making them an excellent fit for mathematical applications where complex calculations are required.

OpenAPI Specifications

Effective API design is vital for ensuring usability and maintainability. OpenAPI specifications provide a standardized way to describe API functionalities, including endpoints, input, and output data structures.

Understanding OpenAPI

OpenAPI allows developers to define the full functionality of APIs in a standard format, using a YAML or JSON document. Defining an API with OpenAPI could include roots-related functionalities, ensuring clarity and accessibility.

openapi: 3.0.0
info:
  title: Root Calculation API
  version: 1.0.0
paths:
  /calculate-root:
    get:
      summary: Calculate the n-th root of a number
      parameters:
        - name: number
          in: query
          description: The number to find the root of
          required: true
          schema:
            type: number
        - name: n
          in: query
          description: The root degree
          required: true
          schema:
            type: integer
      responses:
        '200':
          description: Successfully calculated the root
          content:
            application/json:
              schema:
                type: object
                properties:
                  root:
                    type: number

This document can lead to the seamless creation of an API endpoint dedicated to root calculations, enabling other applications to call on this functionality.

Benefits of Using OpenAPI

1. Consistency: Ensures that APIs maintain a consistent structure, making it easier for developers to integrate.
2. Documentation Generation: Automatically generates documentation based on the specification, aiding developers in understanding how to utilize the API effectively.
3. Interoperability: Facilitates easier integration between different services, ensuring the smooth exchange of data.

API Gateways: Streamlining Communication

API gateways serve as intermediaries between clients and back-end services. They handle requests, aggregate results, and manage functionalities such as security, rate limiting, and authentication.

Importance of API Gateways

1. Request Routing: API gateways direct requests to the appropriate service, ensuring efficiency in resource utilization.
2. Security: Implement user authentication and secure API communications, significantly reducing the attack surface.
3. Load Balancing: Distribute client requests effectively across multiple instances of services.

Utilizing APIPark as an API Gateway

Within the context of API management, APIPark stands out as a comprehensive platform.

• Quick Integration of Multiple Services: APIPark helps integrate more than 100 AI models, making it seamless to invoke and utilize mathematical functionalities, including roots calculations, via simple API calls.
• Unified API Format: This standardization eases the invocation of various computation models while reducing maintenance costs, affecting root calculations positively.

Feature	Benefit
Quick Integration	Facilitates the addition of multiple services effortlessly
Unified API Format	Simplifies request processes, reducing complexity
End-to-End API Lifecycle Management	Streamlines the process from inception to decommissioning

With features such as end-to-end API lifecycle management, APIPark enhances the efficiency of routing requests pertinent to mathematical root calculations.

Conclusion

Understanding 3.4 as a root involves exploring both its mathematical implications and practical applications in the realm of algorithms, particularly where APIs and OpenAPI specifications are concerned. With an emphasis on efficient management through API gateways, tools like APIPark provide flexible, reliable platforms for integrating such functionalities into software applications.

Mastering these concepts will not only strengthen one’s grasp of mathematical principles but also elevate how effectively these principles can be applied in modern programming environments.

Frequently Asked Questions (FAQ)

1. What are roots in mathematics? Roots represent values that, when substituted into an equation, yield a true statement.
2. How is 3.4 significant in programming? In programming, 3.4 can represent thresholds, decision boundaries, or critical points in algorithms involving mathematical equations.
3. What is an API? An API (Application Programming Interface) is a set of protocols for building and integrating software applications, enabling them to communicate with one another.
4. What is OpenAPI? OpenAPI is a specification for defining APIs in a standard format, allowing for improved documentation and integration processes.
5. How does APIPark facilitate API management? APIPark provides a suite of tools for integrating, managing, and deploying APIs, enhancing efficiency and security while streamlining the entire API lifecycle.

🚀You can securely and efficiently call the OpenAI API on APIPark in just two steps:

Step 1: Deploy the APIPark AI gateway in 5 minutes.

APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.

curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh

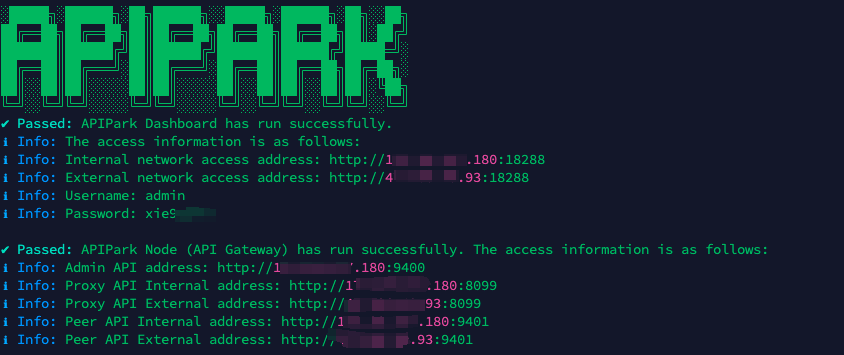
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.

Step 2: Call the OpenAI API.

Learn more