Understanding 3.4 as a Root: A Comprehensive Guide

Introduction
In mathematics, roots play a pivotal role in understanding various functions and equations. Among various roots, the square root and cube root are widely recognized, but there are more complex roots that provide deeper insights, such as the root with the number 3.4. In this comprehensive guide, we will dissect the concept of 3.4 as a root, explore its applications, and illustrate its significance through clear examples. This exploration will also touch upon technical aspects involving APIs—primarily focusing on the functionalities of API gateways like APIPark to facilitate efficient management of integrations and data retrieval.
Understanding Roots
To comprehend the concept of roots, let's revisit some foundational definitions. A root of a number ( x ) is a value that, when raised to a specified power, returns ( x ). For example, the square root of 4 is 2 because ( 2^2 = 4 ). Similarly, the cube root of 27 is 3, as ( 3^3 = 27 ).
In this context, we focus on the decimal representation, such as 3.4. To dissect the nature of 3.4 as a root, we consider its representation in radical form. Specifically, we may express it as the 3.4-th root of a number ( x ).
Mathematical Representation of 3.4 as a Root
Mathematically, expressing 3.4 as a root can be shown through the following equation:
[ y = x^{\frac{1}{3.4}} ]
Where: - ( y ) = the 3.4-th root of ( x ) - ( \frac{1}{3.4} ) = the exponent representing the modification to reach the root
This relationship illustrates that to find the 3.4-th root of any number ( x ), we simply raise ( x ) to the power of ( \frac{1}{3.4} ).
APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇
The Significance of 3.4 Roots in Various Applications
The impact of understanding decimal roots extends beyond theoretical mathematics. It has practical applications in numerous fields such as physics, engineering, finance, and data science.
Applications in Physics
In physics, specifically in the realm of kinematics, the concept of root refers to time taken for an object to traverse specific distances under uniform acceleration. For instance, an acceleration described by a cubic function can lead to calculations involving roots, including fractional roots like 3.4 when determining distances or speeds over specific intervals.
Applications in Engineering
Engineers frequently utilize root calculations when dealing with cubic equations. Many designs and structural analyses depend on accurately estimating roots to ensure stability and efficiency in constructions. For instance, the calculation of moments of inertia can involve roots to ascertain the rigidity of materials under stress.
Applications in Finance and Data Science
In financial modeling, roots are indispensable in risk assessment and in determining compound interest. For example, calculating the rate over a different number of compounding periods might yield a scenario where 3.4 emerges as an important root. Similarly, in data science, algorithms for machine learning and predictive analysis can leverage roots for feature scaling, where transformations involving roots can stabilize variance and normalize distributions.
Exploring API and its Integration with Mathematical Functions
To efficiently handle mathematical functions and algorithms, especially in programming, Application Programming Interfaces (APIs) come into play. APIs are crucial for software interactions, allowing different applications to communicate seamlessly.
The Role of API Gateways
An API gateway acts as a management tool for API requests. It manages traffic routing, security provisions, and handles various integrations, ensuring that data flows efficiently between applications. This aligns perfectly with complex calculations like those involving roots.
Introducing APIPark
One tool that simplifies the management of such integrations is APIPark, an open-source AI gateway and API management platform. APIPark provides developers with various tools and functionalities to streamline API management processes.
| Feature | Description |
|---|---|
| Quick Integration | Seamless integration of 100+ AI models |
| Unified API Format | Standardizes request data across all models |
| Prompt Encapsulation | Combines AI models with custom prompts |
| End-to-End Lifecycle Management | Manages API design, publication, and decommission |
| Team Sharing | Centralized display of API services |
| Independent Permissions | Customized access for each team (tenant) |
| Performance | Achieves high TPS metrics |
| Call Logging | Comprehensive API call logging |
| Powerful Data Analysis | Analyzes historical call data for trends |
By embracing tools like APIPark, developers can maximize efficiency during their mathematical operations and data retrieval tasks. The platform simplifies maintaining the APIs necessary for executing functions like extracting roots and other complex mathematical operations.
Examples of 3.4 as a Root in Calculations
Now that we have established the theoretical basis of 3.4 as a root, it is imperative to provide illustrative examples to enhance understanding.
Example 1: Calculating the 3.4-th Root of a Number
Let us compute the 3.4-th root of 100. Using the formula we described:
[ y = 100^{\frac{1}{3.4}} \approx 3.98 ]
This value indicates that, when raised to the power of 3.4, it approximates to 100, showcasing the alignment with numerical representation.
Example 2: Application in Cubic Functions
If we consider a cubic function where ( f(x) = x^3 - 27), we can find the root of this function using numerical analysis. Here, we determine:
[ x = 3 ]
With our equation adjusted to consider fractional roots, we can explore roots leading up to 3.4, revealing how adjustment in roots can yield different realizations of the output.
The Significance of Accuracy in Root Calculations
Precision is vital in mathematical calculations—especially when programming algorithms or developing software solutions. Mistakes in determining roots may lead to erroneous outputs, causing a ripple effect in applications ranging from engineering to finance. This makes integrating accurate mathematical libraries and protocols essential.
API Management in Various Mathematical Applications
Integrating API functionalities with mathematical computations provides several benefits. For example, allowing external applications to access root calculation methods via APIPark enhances collaboration between software. This means a finance application might request a root calculation for risk assessment seamlessly through an API call.
Conclusion
Understanding 3.4 as a root opens up a world of mathematical insights and applications across various fields including physics, engineering, finance, and data science. The integration of such calculations into software applications facilitated by tools like APIPark emphasizes the importance of utilizing technological advancements to streamline processes, improve accuracy, and enhance operational efficiency.
Frequently Asked Questions (FAQs)
- What is the significance of 3.4 as a root?
- The significance lies in its application across various domains, including physics, engineering, and data science, offering accurate calculations for diverse functions.
- How is the 3.4-th root calculated?
- The calculation involves raising the number to the power of ( \frac{1}{3.4} ).
- Can APIs be used to simplify mathematical calculations?
- Yes, APIs can facilitate complex calculations by allowing applications to access functions and operations as services.
- What is APIPark?
- APIPark is an open-source AI gateway and API management platform designed to help developers manage and integrate APIs efficiently.
- Why is root calculation important in finance?
- Root calculations are essential for understanding compound interest and risk assessments, which are critical for financial decisions.
🚀You can securely and efficiently call the OpenAI API on APIPark in just two steps:
Step 1: Deploy the APIPark AI gateway in 5 minutes.
APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.
curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh
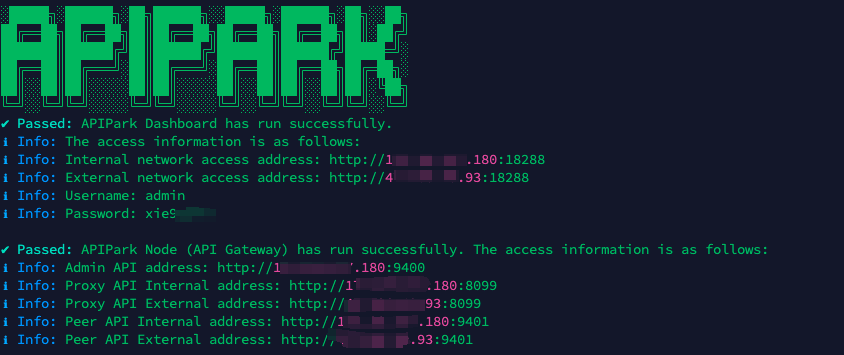
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.
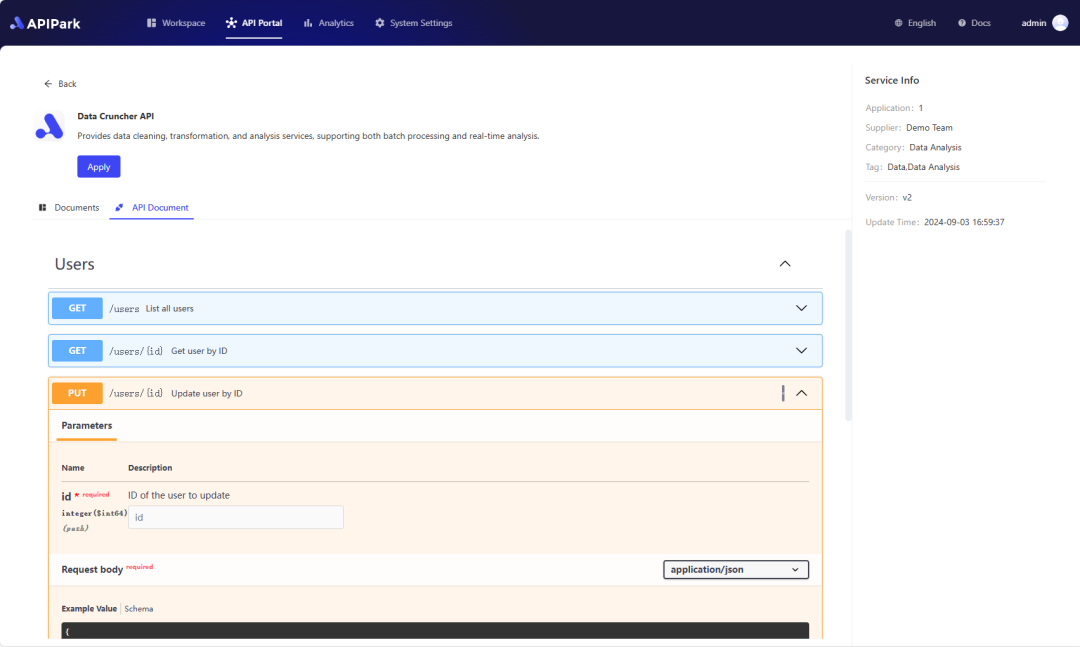
Step 2: Call the OpenAI API.