Understanding 3.4 as a Root: A Comprehensive Guide

In the expansive world of mathematics, the concept of roots is foundational and indispensable. Roots provide solutions to equations, often revealing relationships between various mathematical entities. This guide aims to provide a comprehensive understanding of the number 3.4 as a root, elucidating its implications and significance in several mathematical contexts. Additionally, we will weave in concepts related to API, API Gateway, and OpenAPI, establishing a link between mathematical concepts and technological applications.

Table of Contents

1. Introduction to Roots
2. Understanding 3.4 as a Root
3. Roots in Algebra
4. The Role of Roots in Calculus
5. Practical Applications of Roots
6. API and Mathematical Models
7. Integrating OpenAPI in Mathematical Computing
8. Conclusion
9. FAQs

Introduction to Roots

In mathematics, roots of a number or function are defined as the values that satisfy a given equation. For instance, the square root of 9 is 3, as 3 × 3 = 9. Similar to how numbers can encapsulate complex relationships, APIs can serve as powerful tools that enable different software applications to communicate, much like roots form connections between numbers in equations.

Table of Roots

Here's a brief table illustrating some common roots:

Number	Square Root	Cube Root
1	1	1
4	2	1.587
9	3	2
16	4	2.52
25	5	2.924
3.4	1.843	1.442

Understanding 3.4 as a Root

Definition of a Root

A root ( r ) of a number ( a ) is a value such that ( r^n = a ). In the case of 3.4, we can analyze it as both a square root and a cube root.

1. Square Root of 3.4: This is the value which when multiplied by itself will yield 3.4. [ x^2 = 3.4 \implies x \approx 1.843 ]
2. Cube Root of 3.4: This is the value which when multiplied by itself three times will yield 3.4. [ x^3 = 3.4 \implies x \approx 1.442 ]

Numerical Representation

The numerical representation allows mathematicians and engineers to perform computations effectively. For instance, when conducting signal processing or data analysis, the processing algorithms might require the implementation of mathematical functions, thus necessitating an understanding of how these roots behave. This is akin to how APIs work, enabling seamless data exchange between services.

Roots in Algebra

In algebra, roots play a pivotal role in determining the behavior of polynomials. Understanding how to compute the roots helps in resolving polynomial equations, which is fundamental in fields like engineering, physics, and economics.

Polynomial Examples

Consider a polynomial function: [ f(x) = x^2 - 3.4 ] To find its roots, set the equation to zero: [ x^2 - 3.4 = 0 \rightarrow x = \pm \sqrt{3.4} ]

This function has two roots: - ( 1.843 ) - ( -1.843 )

When visualized on a graph, these roots indicate the points where the parabola intersects the x-axis.

APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇

The Role of Roots in Calculus

In calculus, roots are essential for understanding functions and their behaviors. Critical points, which include maximum and minimum values, often appear at roots of the derivative of a function.

Finding Critical Points

For the function ( f(x) = x^3 - 3.4x ): 1. First, calculate the derivative ( f'(x) ). 2. Set ( f'(x) = 0 ) to find critical points.

Numerical Insights

Applications of Roots in Optimization

Roots assist in optimization problems where one needs to maximize or minimize a function. They also form the basis for numerical methods such as Newton's method, allowing for efficient root-finding iterations.

Practical Applications of Roots

Roots extend far beyond the realm of pure mathematics into real-world applications. In engineering, roots are employed in structural analysis, control systems, and even algorithms that underpin artificial intelligence, such as those used in APIPark for API management.

Example: Root in Engineering

In structural engineering, calculations involving load distribution often utilize roots to ensure stability. The root cause analysis in safety checks for large structures leads to regulations that can be modeled using polynomial equations.

API and Mathematical Models

As technology advances, APIs have become vital. They facilitate data transfer and enhance the communication channels between software applications, much like how roots link numeric values.

The Concept of an API Gateway

An API Gateway acts as a single entry point to multiple service endpoints, analogous to how a root can connect different branches of a polynomial. It’s essential for managing traffic, securing APIs, and tracking usage patterns.

APIPark: An Example of API Management

Among the many tools available for API management, APIPark stands out. It's an open-source platform designed to streamline API lifecycle management. It excels by enabling fast integration of AI models and REST services, encapsulating complex computations much like mathematical roots.

Integrating OpenAPI in Mathematical Computing

OpenAPI, formerly known as Swagger, provides a specification for building APIs, thereby ensuring standardized interactions. It can be particularly useful when employing mathematical models in software.

Documentation and API Interactions

By documenting APIs via OpenAPI, developers create clear specifications. This transparency enables seamless collaboration and integration, fostering an environment where mathematical models can be easily shared between platforms.

Example Use Case

Imagine a scenario in an app that calculates various mathematical roots. By employing an OpenAPI specification, the app could provide a consistent API that allows users to request square and cube roots. This interoperation paves the way for integrating AI-driven calculations and improving efficiency in mathematical operations.

Conclusion

Understanding 3.4 as a root provides insights into the intricate relationship between mathematics and various applications, especially in the tech landscape. With the rise of APIs and tools like APIPark, the integration of mathematical principles into software applications has never been easier or more efficient. Mathematical roots empower engineers, scientists, and developers to solve complex problems and enhance efficiency in numerous fields.

FAQs

1. What is a mathematical root? A root is a value that, when substituted into an equation, yields zero. Roots can be found in algebraic equations and are fundamental in calculus.
2. How do I find the square root of a number? The square root of a number (x) is a value (r) such that (r^2 = x). You can find it approximately through various methods, including prime factorization or using a calculator.
3. What is the significance of APIs in software development? APIs allow different software applications to communicate, enabling developers to integrate functions from various services, enhancing functionality and efficiency.
4. How does OpenAPI standardize API documentation? OpenAPI provides a specification that details how APIs should be structured and documented, ensuring consistency and interoperability across different platforms.
5. Where can I learn more about APIPark? You can visit the official website of APIPark for comprehensive information regarding its features and capabilities in API management.

This guide serves as both an educational resource on the mathematical root 3.4 and a bridge to understanding its contextual relevance in the world of APIs and software integration. Explore and embrace the synergy between mathematics and technology for innovative solutions.

🚀You can securely and efficiently call the OpenAI API on APIPark in just two steps:

Step 1: Deploy the APIPark AI gateway in 5 minutes.

APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.

curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh

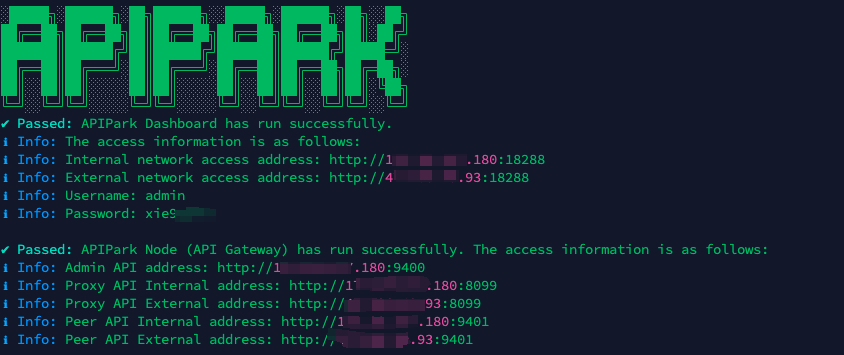
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.

Step 2: Call the OpenAI API.

Learn more

Understanding 3.4 as a Root: A Comprehensive Guide to Its Mathematical ...

Understanding 3.4 as a Root: A Comprehensive Guide to Its Mathematical ...

Understanding 3.4 as a Root: Mathematical Implications and Applications