Murmur Hash 2 Online: Fast & Free Hash Calculator

In the vast and ever-expanding landscape of modern computing, where data flows ceaselessly and efficiency is paramount, the role of seemingly simple yet profoundly powerful algorithms cannot be overstated. Among these foundational elements, hashing functions stand as silent workhorses, underpinning countless systems from databases and caching layers to network protocols and distributed computing architectures. They provide an indispensable mechanism for rapidly processing, indexing, and verifying data, acting as a cornerstone of performance and integrity in an increasingly data-driven world. Within this critical domain, the Murmur Hash 2 algorithm has carved out a significant niche, celebrated for its exceptional speed and excellent distributional properties, making it a go-to choice for a wide array of non-cryptographic applications.

The demand for efficient, reliable, and easily accessible tools to interact with these algorithms is as persistent as the algorithms themselves. This is where "Murmur Hash 2 Online: Fast & Free Hash Calculator" emerges as an invaluable resource. In an era where developers, system administrators, data analysts, and even curious enthusiasts constantly seek quick solutions without the overhead of local software installations or complex programming environments, an online calculator offers unparalleled convenience. It democratizes access to sophisticated hashing capabilities, enabling immediate computation and verification of hash values directly from a web browser. This comprehensive guide will delve deep into the intricacies of Murmur Hash 2, exploring its origins, its technical brilliance, its myriad applications, and ultimately, the immense utility of a fast and free online tool that brings this powerful algorithm directly to your fingertips. We will uncover why Murmur Hash 2 remains a relevant and highly regarded choice for non-cryptographic hashing, and how online calculators streamline its application in practical scenarios, ensuring both efficiency and accessibility for a global audience.

Understanding the Fundamentals of Hashing

Before we embark on a detailed exploration of Murmur Hash 2, it is crucial to establish a solid understanding of what hashing entails and why it is so fundamental to modern computing. At its core, a hash function is a mathematical algorithm that takes an input (or 'message' or 'key') of arbitrary length and returns a fixed-size string of bytes, typically a hexadecimal number, known as a 'hash value', 'hash code', 'digest', or simply 'hash'. Think of it as a unique digital fingerprint for any given piece of data.

The primary characteristics that define a good hash function are critical to its utility:

1. Determinism: For a given input, a hash function must always produce the exact same output hash value. Any deviation would render it useless for verification or lookup purposes. This consistency is the bedrock upon which all hashing applications are built.
2. Fixed-Size Output: Regardless of whether the input is a single character, a paragraph, an entire book, or a multi-gigabyte file, the hash function will always generate a hash value of a predetermined length. This fixed-size output is essential for efficient storage and comparison of hash values.
3. Computational Efficiency (Speed): A hash function should be computationally fast to execute. The quicker it can generate a hash, the more effective it becomes in high-throughput applications where speed is a critical performance metric, such as data indexing, caching, and network routing.
4. Good Distribution (Avalanche Effect): A small change in the input data (even a single bit flip) should result in a significantly different hash value. This property, often referred to as the 'avalanche effect', ensures that hash values are uniformly distributed across the entire range of possible outputs, minimizing patterns and making it harder to predict outputs or craft inputs that produce specific hashes. A well-distributed hash helps reduce collisions in hash tables.
5. Collision Resistance (to a degree): A 'collision' occurs when two different inputs produce the same hash value. While perfect collision resistance is mathematically impossible for any hash function (as there are infinitely more possible inputs than fixed-size outputs), a good hash function should make it computationally very difficult or improbable to find two different inputs that hash to the same value. The degree of collision resistance required varies significantly between cryptographic and non-cryptographic hashes.

It's important to distinguish between the two primary categories of hash functions:

• Cryptographic Hash Functions: These are designed with stringent security requirements, making it computationally infeasible to reverse the hash (find the original input from the hash) or to find collisions. Examples include SHA-256, SHA-3, and MD5 (though MD5 is now considered insecure for cryptographic purposes). They are used for digital signatures, password storage, data integrity checks in secure contexts, and blockchain technologies.
• Non-Cryptographic Hash Functions: These prioritize speed and good distribution over extreme collision resistance or one-way properties. While they aim to minimize collisions in typical use cases, they are not designed to withstand malicious attacks aimed at finding collisions. Murmur Hash 2 falls squarely into this category. Their primary applications include hash tables, bloom filters, unique ID generation, and data partitioning, where performance is key and the threat of adversarial collision attacks is low or irrelevant.

The necessity of hashing permeates nearly every layer of modern software infrastructure. In databases, hash values are often used to quickly locate records. In caching systems, hashes serve as keys to rapidly retrieve cached data. In distributed systems, consistent hashing helps distribute data or requests evenly across a cluster of servers. For data integrity, comparing hash values of a file before and after transmission can quickly confirm if the data was corrupted. Without these underlying hashing mechanisms, many of the fast, responsive, and robust digital services we rely upon daily would simply not be feasible. Understanding these fundamentals sets the stage for appreciating the ingenious design and immense practical value of algorithms like Murmur Hash 2.

The Genesis and Evolution of Murmur Hash

The Murmur Hash algorithm, a name that subtly hints at its internal mixing process, was conceived and developed by Austin Appleby, an individual recognized for his contributions to efficient algorithms in computing. Its inception was driven by a pressing need for a non-cryptographic hash function that could deliver superior performance—specifically, exceptional speed and excellent statistical distribution—compared to existing alternatives at the time, without the overhead of cryptographic strength. Appleby’s goal was to create a hash that was "fast for general hash loads, especially for 32-bit platforms, and good for hash tables," focusing on generating distinct hash values with minimal collisions for keys that differ only slightly.

The original Murmur Hash algorithm (sometimes retrospectively referred to as Murmur Hash 1) was designed to address shortcomings in commonly used non-cryptographic hashes of the era. Many existing hashes, while simple, often exhibited poor distribution characteristics, leading to an increased number of collisions when faced with certain data patterns. This could significantly degrade the performance of hash tables and other hash-dependent data structures. Appleby recognized that a good hash function for these purposes needed to quickly "mix" the input bits in such a way that even minor variations in input produced dramatically different outputs, effectively scrambling the data to achieve uniform distribution.

The "Murmur" name itself is somewhat evocative of the algorithm's internal workings. It's often associated with the 'mul' (multiply) operations that are central to its mixing stages. The algorithm uses a series of carefully chosen multiplication and bitwise rotation/shift operations, interspersed with XORs, to thoroughly scramble the input data. This complex but highly optimized mixing process is what gives Murmur Hash its excellent statistical properties, creating a "murmur" or complex sound (in this case, a complex bit pattern) from a simple input.

From Murmur Hash 1 to Murmur Hash 2: A Leap Forward

The transition from Murmur Hash 1 to Murmur Hash 2 represented a significant refinement and improvement in Appleby's design. While Murmur Hash 1 was already quite effective, further research and analysis revealed opportunities to enhance its speed, distribution quality, and collision resistance. Murmur Hash 2 was specifically optimized for 32-bit platforms, where it achieved remarkable performance, often outperforming many other non-cryptographic hashes while maintaining superior distribution.

Key improvements and design considerations in Murmur Hash 2 included:

• Refined Mixing Operations: The constants, shifts, and multiplication factors used in Murmur Hash 2 were meticulously chosen after extensive testing and analysis. These "magic numbers" are not arbitrary; they are the result of mathematical exploration aimed at maximizing the avalanche effect and minimizing statistical biases. The interplay of multiplication with specific large prime numbers and bitwise shifts is central to its ability to spread entropy efficiently.
• Emphasis on Speed: Murmur Hash 2 was engineered to be extremely fast, leveraging simple, CPU-friendly operations that can be executed rapidly. Its design avoids complex conditional branches or memory accesses that could introduce latency. This focus on raw speed, without compromising distribution quality, made it particularly attractive for applications where every clock cycle counts.
• Excellent Statistical Properties: Through rigorous testing, Murmur Hash 2 demonstrated superior distribution characteristics for various types of input data, including highly patterned or similar keys. This translates directly into fewer collisions in hash tables, which in turn leads to better average-case performance for data structures that rely on hashing. A lower collision rate means faster lookups, insertions, and deletions.
• Simplicity of Implementation: Despite its sophisticated mathematical underpinnings, the core Murmur Hash 2 algorithm is relatively straightforward to implement, making it easy for developers to integrate into their projects. This ease of adoption further contributed to its widespread use.

Austin Appleby’s design goals for Murmur Hash 2 were clear: provide a general-purpose, non-cryptographic hash function that is exceptionally fast, produces high-quality hash values with good distribution, and is robust enough for a wide range of practical applications. His success in achieving these goals solidified Murmur Hash 2's reputation as a reliable and high-performance hashing algorithm, setting a new benchmark for efficiency in its class. Its widespread adoption by major technology companies and open-source projects underscores its enduring value and the brilliance of its original design. The careful balance between computational frugality and statistical robustness is what truly distinguishes Murmur Hash 2 in the crowded field of hashing algorithms.

Deep Dive into the Murmur Hash 2 Algorithm

To truly appreciate the elegance and efficiency of Murmur Hash 2, it's beneficial to delve into its algorithmic structure. While a full bit-by-bit implementation detail can be quite complex, understanding the core components and the general flow provides significant insight. Murmur Hash 2 (and its close variant MurmurHash2A) operates in stages, meticulously processing the input data to produce a highly mixed, fixed-size hash value.

The algorithm typically processes data in blocks, usually 4 bytes (32-bit) or 8 bytes (64-bit) at a time, performing a series of multiplications, bit shifts, and XOR operations. This iterative mixing ensures that every bit of the input contributes to the final hash in a non-linear fashion, maximizing the avalanche effect.

Core Components and Algorithmic Flow

Let's break down the general process for a 32-bit Murmur Hash 2, which is one of the most common variants:

1. Initialization:
   • The hash function starts with an initial seed value. This seed is a 32-bit integer that can be specified by the user. A different seed will produce a different hash for the same input, which is useful for situations like combining hashes or generating multiple distinct hash values for the same data. If no seed is specified, a default value (often 0 or a fixed constant) is used.
   • A primary hash variable, let's call it h, is initialized to the seed value.
   • Two "magic numbers" are central to the Murmur Hash 2 algorithm: m and r. These are constants carefully chosen for their statistical properties.
     • m (multiplier): A large odd number (e.g., 0x5bd1e995 for 32-bit). Multiplication by m is crucial for scattering bits and enhancing distribution. Multiplying by an odd number ensures that all bits of the multiplied value are affected, unlike even numbers which can drop information.
     • r (rotation amount): A small integer (e.g., 24 for 32-bit). This value determines how many bits the current hash value is rotated right by, ensuring bits from higher and lower positions interact.
2. Processing in Blocks:
   • The input data is processed in chunks, typically 4 bytes at a time (for a 32-bit hash).
   • The algorithm iterates through the input data, taking each 4-byte chunk as a k (key) value.
   • For each k:
     • k = k * m; (Multiply the current 4-byte chunk by the constant m). This is a crucial mixing step.
     • k = k ^ (k >> r); (XOR the k with itself shifted right by r bits). This further shuffles the bits within k.
     • k = k * m; (Multiply k by m again). Another mixing step, ensuring thorough scrambling.
     • h = h * m; (Multiply the main hash h by m).
     • h = h ^ k; (XOR the main hash h with the processed k). This combines the processed input chunk into the accumulating hash value.
   • This loop continues until all full 4-byte blocks of the input have been processed.
3. Handling the Tail (Remaining Bytes):
   • If the input data length is not a perfect multiple of 4 bytes, there will be a 'tail' of 1, 2, or 3 bytes remaining. The algorithm handles these remaining bytes individually to ensure every bit of the input contributes to the hash.
   • A switch statement is typically used to process the tail bytes:
     • If 3 bytes remain: The third byte is XORed into h, then h is multiplied by m.
     • If 2 bytes remain: The second byte is XORed into h, then h is multiplied by m.
     • If 1 byte remains: The first byte is XORed into h, then h is multiplied by m.
   • The m multiplication after each tail byte ensures that even these final few bits are thoroughly mixed into the hash.
4. Finalization Mix:
   • After all input blocks and tail bytes have been processed, a final mixing step is applied to the accumulated h value. This "finalizer" ensures that all bits of h are thoroughly mixed, reducing potential biases from the block processing stage and improving distribution.
   • A typical finalization mix for 32-bit Murmur Hash 2 involves a series of XORs with right shifts and multiplications:
     • h ^= h >> 13;
     • h *= m;
     • h ^= h >> 15;
   • These final steps further distribute the entropy throughout the hash value, producing a high-quality final hash.

Understanding the "Magic Numbers"

The constants m and r are not arbitrary. Austin Appleby, through extensive research and analysis of hash function properties, selected these values to optimize for specific criteria:

• m (Multiplier): The choice of 0x5bd1e995 (for 32-bit) is a large prime number with specific bit patterns. Multiplying by such a constant helps to mix bits effectively across the entire 32-bit range. The use of an odd multiplier is vital because it preserves all information during multiplication, preventing bits from being lost or zeroed out, which can happen with even multipliers. This aggressive multiplication is a key factor in Murmur Hash 2's rapid mixing and excellent distribution.
• r (Rotation Amount): The rotation constant (e.g., 24 for 32-bit) determines how bits are shifted. Rotations are crucial because they ensure that bits from different positions in the input k interact with each other and are spread throughout the hash value, preventing positional biases.

MurmurHash2 vs. MurmurHash2A (Incremental Version)

It's also worth noting the distinction between MurmurHash2 and MurmurHash2A. * MurmurHash2 processes the entire input data at once, as described above. * MurmurHash2A is an incremental version, often used when the input data is streamed or not available entirely at once. It essentially updates the hash state with each new chunk of data without needing to re-process previous data. This is achieved by slightly altering the update step for h to h ^= (k * m); h *= m;, which is more suitable for cumulative hashing. The finalization step remains similar. MurmurHash2A is often preferred in scenarios where data comes in arbitrary-sized blocks or needs to be hashed incrementally.

64-bit MurmurHash2

There also exists a 64-bit version of Murmur Hash 2, which produces a 64-bit hash value. This variant follows the same principles but uses 64-bit arithmetic, different m and r constants optimized for 64-bit operations (e.g., m = 0xc6a4a7935bd1e995ULL), and processes data in 8-byte blocks. The 64-bit version is particularly useful for systems dealing with larger datasets or requiring a broader hash space to minimize collisions further.

The intricate dance of multiplications, shifts, and XORs, carefully choreographed by the constants m and r, is what gives Murmur Hash 2 its remarkable speed and statistical robustness. Its design is a testament to the power of well-chosen bitwise operations in creating highly efficient and effective hashing algorithms. By understanding these inner workings, one can better appreciate why Murmur Hash 2 remains a highly regarded choice for non-cryptographic hashing in a wide range of demanding applications.

Advantages and Limitations of Murmur Hash 2

Murmur Hash 2, while a highly optimized and widely respected hash function, is not a panacea for all hashing needs. Its design prioritizes specific characteristics, leading to distinct advantages in certain use cases, but also inherent limitations that must be understood. A clear grasp of these aspects is crucial for making informed decisions about its suitability for a given application.

Key Advantages of Murmur Hash 2

1. Exceptional Speed: This is arguably the most celebrated attribute of Murmur Hash 2. It was designed from the ground up to be incredibly fast, especially on 32-bit architectures. Its operations largely consist of simple bit shifts, XORs, and multiplications, which modern CPUs can execute with extreme efficiency. This makes it ideal for high-throughput scenarios where data needs to be hashed rapidly, such as in network packet processing, real-time analytics, or large-scale data indexing. Its performance often significantly surpasses other non-cryptographic hashes like FNV or DJB2, and even some cryptographic hashes (though for different purposes).
2. Excellent Statistical Distribution: Murmur Hash 2 produces hash values that are very well distributed across the entire output range, even for input keys with high entropy or highly similar patterns (e.g., strings that differ by only a few characters). This "goodness" of distribution is vital for hash tables and other hash-based data structures. A uniform distribution minimizes hash collisions, leading to fewer chains or probes, which in turn results in faster average-case performance for lookups, insertions, and deletions. Poorly distributed hashes can degenerate hash table performance to linear search speeds, negating their primary benefit.
3. Good Collision Resistance (for non-cryptographic uses): While not cryptographically secure, Murmur Hash 2 offers strong collision resistance for its intended domain. It's difficult to find two arbitrary inputs that hash to the same value through brute force or random chance. This level of collision resistance is more than sufficient for applications like bloom filters, cache key generation, and distributed system partitioning, where the primary concern is accidental collisions rather than malicious attempts to generate them.
4. Small Code Footprint and Simple Implementation: The core Murmur Hash 2 algorithm is relatively concise and straightforward to implement in various programming languages. This simplicity contributes to its speed and makes it easy to integrate into existing projects without adding significant complexity or dependencies. Its well-defined nature ensures consistent results across different implementations if the constants and logic are followed.
5. Proven Track Record and Widespread Adoption: Murmur Hash 2 has been widely adopted by major technology companies and open-source projects (e.g., used in Hadoop, Cassandra, libmemcached). Its extensive use in demanding, high-performance environments serves as a testament to its reliability and effectiveness. This broad adoption also means it has been rigorously tested and battle-hardened over many years.

Limitations and When Not to Use Murmur Hash 2

Despite its compelling advantages, Murmur Hash 2 has specific limitations that define its appropriate use cases:

1. Not Cryptographically Secure: This is the most critical limitation. Murmur Hash 2 is explicitly designed as a non-cryptographic hash function. It is relatively easy to find collisions if one is actively trying to do so. An attacker could craft multiple inputs that produce the same hash value, which could be exploited in security-sensitive contexts. Therefore, Murmur Hash 2 must not be used for:
   • Password storage: Use strong cryptographic hashes like Argon2, bcrypt, or scrypt.
   • Digital signatures or message authentication codes (MACs): Use SHA-256/SHA-3 with HMAC.
   • Data integrity checks where data tampering is a concern: For example, verifying software downloads where malicious modification is possible.
   • Blockchain technologies: These require robust collision resistance against adversarial attacks.
2. Susceptible to Collision Attacks: Because it's not cryptographically secure, Murmur Hash 2 is vulnerable to deliberately crafted collision attacks. If an adversary can control the input data being hashed, they could potentially generate collisions to exploit weaknesses in systems that rely on the hash for security purposes, such as denial-of-service attacks on hash tables.
3. Specific Use Cases: While excellent for its intended purpose, Murmur Hash 2 is not a general-purpose replacement for all other hashing algorithms. For example, it doesn't offer the extreme robustness against all types of input biases that some newer non-cryptographic hashes (like CityHash or xxHash) claim, although its performance-to-quality ratio remains outstanding. For very short keys or highly specific data structures, other specialized hashes might offer marginal advantages, but Murmur Hash 2 remains a strong contender.

In summary, Murmur Hash 2 excels where speed and good statistical distribution are paramount, and the threat of adversarial collision attacks is negligible. It's a workhorse for internal system optimizations, data structuring, and rapid identification. However, any application requiring cryptographic security or robust protection against malicious collision attempts must look to dedicated cryptographic hash functions. Understanding this distinction is key to leveraging Murmur Hash 2 effectively and securely within its intended operational domain.

Real-World Applications of Murmur Hash 2

The robust performance and excellent distributional properties of Murmur Hash 2 have made it an indispensable tool across a broad spectrum of real-world computing applications. Its ability to generate unique, well-distributed identifiers quickly and reliably allows developers to build more efficient, scalable, and responsive systems. From fundamental data structures to complex distributed architectures, Murmur Hash 2 plays a crucial, often unseen, role.

1. Hash Tables and Hash Maps: This is perhaps the most classic and prevalent application. Hash tables are data structures that store key-value pairs, enabling very fast average-case O(1) time complexity for insertions, deletions, and lookups. The efficiency of a hash table is directly dependent on the quality of its hash function. Murmur Hash 2's superior statistical distribution minimizes collisions, ensuring that items are spread evenly across the table's buckets. This prevents the "worst-case" scenario where many keys map to the same bucket, degrading performance to O(N). Languages and libraries often use Murmur Hash 2 or similar high-quality non-cryptographic hashes for their internal map implementations.
2. Bloom Filters: A Bloom filter is a probabilistic data structure that efficiently tests whether an element is a member of a set. It can tell you if an element might be in the set (with a chance of false positives) or definitely is not in the set. Bloom filters require multiple independent hash functions to map elements to various positions in a bit array. Murmur Hash 2 is an excellent choice for generating these multiple hash values due to its speed and good distribution, which is crucial for minimizing the false positive rate in Bloom filters. Common use cases include checking for visited URLs in web crawlers, quickly looking up items in a database to avoid costly disk I/O, or identifying duplicate entries.
3. Load Balancing and Distributed Systems: In large-scale distributed systems, efficiently distributing data or requests across multiple servers is critical for performance and availability. Consistent hashing, a technique that minimizes the redistribution of keys when nodes are added or removed, often relies on a good hash function to map data items and server nodes onto a virtual ring. Murmur Hash 2 is frequently employed here to generate the hashes for both the data items (e.g., user IDs, session tokens, content IDs) and the server nodes. Its consistent output and uniform distribution ensure that data is spread evenly across the cluster, preventing hot spots and maximizing resource utilization. This is fundamental in systems like Cassandra, DynamoDB, and various caching layers.
4. Cache Key Generation: Caching is a cornerstone of high-performance applications, reducing the need to recompute or retrieve data from slower sources. Effective caching relies on unique and deterministic keys to identify cached items. Murmur Hash 2 is often used to generate these cache keys, especially when the original key is a complex object or a long string. Hashing the complex key into a fixed-size, compact Murmur Hash 2 value provides a fast and efficient way to look up cached data in a hash-based cache store (like Memcached or Redis), ensuring cache hits are as fast as possible.
5. Deduplication: When dealing with large datasets, identifying and removing duplicate records is a common task. Murmur Hash 2 can be used to generate a hash for each record or segment of data. By comparing these hash values, duplicates can be quickly identified without needing to perform byte-by-byte comparisons of potentially large data blocks. This is particularly useful in data warehousing, log processing, and content management systems.
6. Unique ID Generation (Non-Cryptographic): While not for cryptographically secure unique IDs, Murmur Hash 2 can be used to generate relatively unique, fixed-size identifiers for various internal purposes, such as tracing requests in a system, generating session IDs (when combined with other entropy), or creating short, persistent identifiers for objects within a bounded system where collisions are not malicious.
7. Data Partitioning and Sharding: Similar to load balancing, in sharded databases or distributed file systems, Murmur Hash 2 can be used to determine which shard or partition a piece of data should reside on. By hashing a primary key (e.g., user ID, product ID) and then applying a modulo operation (hash % number_of_shards), the system can consistently route data to the correct storage location. This ensures data locality and improves query performance.

In the complex orchestration of API management and AI gateways, platforms designed for high efficiency and scalability, such as APIPark, might leverage robust hashing algorithms like Murmur Hash 2 internally for a variety of operational aspects. For instance, when managing the integration of hundreds of AI models and REST services, APIPark could use hashing to: * Generate unique identifiers for API requests: Each incoming API call might be assigned a Murmur Hash 2 value of its payload or a combination of metadata, enabling quick lookup, logging, and correlation across distributed services. * Optimize internal routing and load balancing: To efficiently route requests to the appropriate backend AI models or services, APIPark could use consistent hashing based on request parameters (e.g., user ID, model ID) to distribute traffic across a cluster of AI inference engines or API service instances. This ensures high performance, minimal latency, and optimal resource utilization, similar to its stated performance of over 20,000 TPS with an 8-core CPU. * Implement internal caching mechanisms: For frequently accessed API responses or processed AI results, Murmur Hash 2 could be used to create cache keys, allowing APIPark to quickly retrieve data from its cache rather than re-invoking an AI model or backend service, thus enhancing overall system responsiveness and reducing operational costs. * Rapid indexing of metadata: With a unified management system for authentication, cost tracking, and end-to-end API lifecycle management, APIPark deals with vast amounts of metadata. Hashing could be employed for quickly indexing and retrieving this metadata, speeding up administrative queries and internal system operations.

These applications highlight Murmur Hash 2's versatility and its critical role in building the backbone of modern, high-performance computing infrastructures. Its efficiency and reliability make it a preferred choice for scenarios where speed and good data distribution are paramount, without the need for cryptographic guarantees.

APIPark is a high-performance AI gateway that allows you to securely access the most comprehensive LLM APIs globally on the APIPark platform, including OpenAI, Anthropic, Mistral, Llama2, Google Gemini, and more.Try APIPark now! 👇👇👇

The Convenience of an Online Murmur Hash 2 Calculator

While understanding the intricate algorithms and their myriad applications is essential, the practical utility often comes down to accessibility. For many users—be they developers prototyping ideas, system administrators troubleshooting issues, data analysts verifying data, or students learning about hashing—the immediate need is often to simply "get the hash" of a particular string or data blob. This is precisely where the concept of an online hash calculator, specifically a "Murmur Hash 2 Online: Fast & Free Hash Calculator," proves to be an invaluable and indispensable tool.

An online hash calculator is a web-based utility that allows users to input data (typically text, but sometimes hexadecimal strings or even file uploads), select a specific hashing algorithm (like Murmur Hash 2), and instantly receive the corresponding hash value as output. It functions as a bridge between complex cryptographic or non-cryptographic algorithms and everyday users, simplifying a process that would otherwise require programming knowledge or specialized software installation.

Why Use an Online Murmur Hash 2 Calculator?

The advantages of using an online tool for Murmur Hash 2 computation are numerous and compelling:

1. Speed and Instant Results: The primary benefit is immediate gratification. You type or paste your input, click a button, and within milliseconds, the hash value appears. There's no compilation time, no script execution, and no waiting. This instant feedback loop is incredibly efficient for quick checks and validations.
2. Accessibility and No Software Installation: As a web-based application, an online calculator requires nothing more than a web browser and an internet connection. There's no software to download, install, or update. This makes it universally accessible from any operating system (Windows, macOS, Linux, Android, iOS) and any device, from desktops to smartphones. It eliminates the overhead and potential security risks associated with installing third-party software.
3. Cross-Platform Compatibility: Because it runs in a browser, an online hash calculator is inherently cross-platform. This is particularly useful for teams working in heterogeneous environments or for individuals who switch between different operating systems.
4. Cost-Effectiveness (Free): Most reputable online hash calculators, including those for Murmur Hash 2, are offered completely free of charge. This makes powerful hashing capabilities accessible to everyone, from individual learners to small businesses, without any financial barrier.
5. Simplicity and Ease of Use: Online tools are typically designed with user experience in mind, featuring clean interfaces and intuitive workflows. You don't need to be an expert in programming or hashing theory to use them; the process is usually as simple as "input -> select -> calculate -> output."
6. Convenient for Learning and Experimentation: For students or those new to hashing, an online calculator provides an excellent sandbox for experimentation. They can quickly see how different inputs affect the hash output, observe the avalanche effect, and gain a practical understanding of how the algorithm behaves without diving into code.
7. Quick Verification and Troubleshooting: Developers might use it to quickly verify hash values generated by their own code, ensuring consistency across different implementations. System administrators might use it to troubleshoot configuration issues related to hash-based identifiers or to check data integrity of small snippets.

Target Audience for Online Hash Calculators

The utility of such a tool extends to a diverse audience:

• Software Developers: For quick testing of hash functions, generating test data, debugging code that uses hashing, or creating unique identifiers on the fly.
• System Administrators: To verify configuration files, check checksums of small data snippets, or debug issues in distributed systems that rely on hashing.
• Data Analysts: To quickly generate hashes for specific data points, identify duplicates in small datasets, or for data validation tasks.
• Students and Educators: As an interactive learning tool to demonstrate the principles of hashing, the avalanche effect, and the practical application of algorithms like Murmur Hash 2.
• Security Professionals (with caution): While not for sensitive data, they might use it to test how certain inputs hash or for quick analysis in non-critical scenarios.
• General Users: Anyone needing to quickly generate a hash value for non-sensitive data without wanting to write code or install software.

The existence of a "fast & free" online Murmur Hash 2 calculator empowers a broad user base to interact with a high-performance hashing algorithm effortlessly. It transforms a potentially technical and complex operation into a simple, accessible web-based task, thereby enhancing productivity and fostering a deeper understanding of essential computing concepts.

How to Use a "Fast & Free" Murmur Hash 2 Online Tool

Utilizing an online Murmur Hash 2 calculator is designed to be a straightforward and intuitive process, requiring minimal technical expertise. The goal is to provide a user-friendly interface that quickly delivers accurate hash values. While specific interfaces might vary slightly between different websites, the core steps remain consistent.

Here’s a general step-by-step guide on how to effectively use a "Fast & Free" Murmur Hash 2 online calculator:

Step 1: Access the Online Calculator

First and foremost, you need to navigate to a reliable and trustworthy online Murmur Hash 2 calculator. A quick search for "Murmur Hash 2 online" or "free hash calculator Murmur" will typically yield several options. Ensure you choose a site that appears reputable and has a clean, user-friendly interface.

Step 2: Input Your Data

Once on the calculator page, you will typically find a large text area or an input field. This is where you will provide the data you wish to hash.

• Text Input: Most commonly, you will paste or type plain text directly into this field. This could be a single word, a sentence, a paragraph, a URL, a JSON string, or any other sequence of characters.
  • Crucial Consideration: Encoding: Be aware of text encoding. The hash value for "hello" might differ if it's interpreted as UTF-8 versus ASCII, for example. Reputable calculators usually default to UTF-8, which is the most common web encoding, but some might offer options to select different encodings. Consistency in encoding is vital for reproducible hash values.
• Hexadecimal Input (Optional): Some advanced calculators might offer an option to input data as a hexadecimal string. This is useful if you have raw byte data represented in hex format (e.g., 48656c6c6f for "Hello"). If this option is available, you would typically toggle a setting or select a specific input type before entering your hex string.
• File Upload (Less Common for Murmur Hash 2, but available for other hashes): While less typical for Murmur Hash 2 (which is primarily for strings and small data blocks), some general hash calculators allow you to upload a file to compute its hash. This is more common for cryptographic hashes like SHA-256 for file integrity checks. If available, you would click a "Choose File" button.

Example Input: For demonstration, let's assume we want to hash the string: The quick brown fox jumps over the lazy dog.

Step 3: Select the Murmur Hash 2 Algorithm

Many online hash calculators support a multitude of hashing algorithms (MD5, SHA-1, SHA-256, FNV, CRC32, etc.). You will need to specifically select "Murmur Hash 2" from a dropdown menu, a list of checkboxes, or a dedicated button. Ensure you choose the correct variant, as sometimes "Murmur Hash 2" and "Murmur Hash 3" are listed separately, and possibly even 32-bit vs. 64-bit Murmur Hash 2. For general purposes, "Murmur Hash 2 32-bit" is a common default.

Step 4: Initiate the Calculation

Once your input is entered and the correct algorithm is selected, locate the "Calculate," "Hash," or "Generate" button and click it. The calculator will then process your input using the Murmur Hash 2 algorithm.

Step 5: Interpret the Output

Almost instantaneously, the calculated Murmur Hash 2 value will appear in an output field.

• Format: The hash value is typically displayed as a hexadecimal string. For a 32-bit Murmur Hash 2, this will be an 8-character hexadecimal string (e.g., AABBCCDD). For a 64-bit version, it would be a 16-character hexadecimal string.
• Seed Value: Some calculators allow you to specify an optional seed value. If you use a non-default seed, make a note of it, as the hash will only be reproducible if the same seed is used.
• Output Consistency: The most crucial aspect of using any hash calculator is output consistency. If you use the same input string (with the exact same characters, including whitespace and line breaks, and the same encoding) and the same algorithm (and seed, if applicable) on any compliant Murmur Hash 2 calculator, you should always get the identical hash output. This deterministic nature is a fundamental property of hash functions.

Example Output: For the input The quick brown fox jumps over the lazy dog. (using a common Murmur Hash 2 32-bit implementation with a default seed of 0), you might get a hash value like: 653D83D4.

By following these simple steps, anyone can quickly and accurately generate Murmur Hash 2 values, leveraging the power of this efficient algorithm without needing to delve into its underlying code. The "fast & free" nature of these online tools makes them an incredibly convenient resource for a wide array of practical tasks.

Security and Best Practices for Online Hashing

While "Murmur Hash 2 Online: Fast & Free Hash Calculator" tools offer unparalleled convenience, it's paramount to approach their usage with an understanding of security implications and adherence to best practices. The very nature of online services means that your input data temporarily traverses the internet and is processed by a third-party server. This inherent characteristic necessitates caution, especially when dealing with any form of sensitive information.

Data Privacy: A Critical Concern

The golden rule for using any online hashing tool, or indeed any online utility that processes user input, is: Never input sensitive or confidential information.

• Avoid Personally Identifiable Information (PII): Do not hash names, email addresses, phone numbers, social security numbers, credit card details, medical records, or any other data that could identify an individual or compromise their privacy. Even if the hash itself is not easily reversible, sending this data to an unknown server poses a risk.
• No Proprietary or Business-Critical Data: Similarly, avoid inputting company secrets, confidential project details, authentication tokens, API keys, or any other data whose exposure could lead to financial loss, intellectual property theft, or operational disruption.
• No Passwords (Even for Testing): Never hash passwords, even for testing purposes. Hash functions, especially non-cryptographic ones like Murmur Hash 2, are not designed to protect sensitive credentials. Even for cryptographic hashes, real password hashing should only occur within secure, server-side environments using established, robust key derivation functions like Argon2, bcrypt, or scrypt.

The risk lies in the possibility that the online service provider might log your inputs, or that the data could be intercepted during transmission (though HTTPS mitigates this significantly). Even if the service claims not to log data, relying on such claims for sensitive information is ill-advised given the potential consequences.

Verify Results and Understand Limitations

• Cross-Verification: If you are using an online calculator to verify a hash value generated by your own code or another system, it's a good practice to cross-verify the hash with at least one other reputable online calculator, or ideally, against a local implementation of Murmur Hash 2. This helps confirm that the online tool is correctly implementing the algorithm and that your local implementation is also consistent.
• Source Code Scrutiny (if available): For the technically inclined, if an online calculator's source code is open-source (e.g., hosted on GitHub), reviewing it can provide an extra layer of confidence regarding its implementation and whether it logs user data.
• Understand Murmur Hash 2's Purpose: Always remember that Murmur Hash 2 is a non-cryptographic hash. Its primary strengths are speed and distribution, not security against malicious attacks. Therefore, its output should never be relied upon for cryptographic security, such as verifying the integrity of sensitive files that might have been tampered with by an adversary, or for generating truly secure unique identifiers.

Best Practices for Responsible Usage

1. Use HTTPS/SSL: Always ensure that the online hash calculator website you are using has a valid SSL certificate and uses HTTPS. This encrypts the communication between your browser and the server, protecting your input data from being intercepted by casual eavesdroppers during transit. Look for the padlock icon in your browser's address bar.
2. Stick to Non-Sensitive Data: Limit your use of online calculators to public data, test strings, or information that holds no intrinsic value if exposed.
3. Local Tools for Production/Sensitive Tasks: For any production system, sensitive data processing, or critical security functions, always use local, self-controlled implementations of hashing algorithms within a secure environment. This could be a library in your application code or a command-line utility on a trusted machine.
4. Awareness of Input Formatting: Be meticulously careful about input formatting. Leading/trailing whitespace, invisible characters, varying line endings (CRLF vs. LF), and character encodings can all subtly alter a hash value. Ensure your input matches exactly what you intend to hash.
5. Be Skeptical of "Super Secure" Claims: Any online tool claiming to provide "super secure" hashing for sensitive data should be viewed with extreme skepticism. True security in hashing requires careful control over the environment and the algorithm's application, which is typically not achievable with a generic public web service.

By adhering to these security guidelines and best practices, users can safely and effectively leverage the immense convenience offered by online Murmur Hash 2 calculators for their appropriate, non-sensitive hashing needs, while mitigating potential risks and ensuring data integrity in critical scenarios.

Murmur Hash 2 in the Broader Hashing Landscape

Murmur Hash 2, despite its age (first released around 2008-2009), continues to hold a significant position in the non-cryptographic hashing landscape. Its blend of speed and distribution quality made it a benchmark for many years, and while newer algorithms have emerged, understanding its place relative to other popular hashes is crucial for choosing the right tool for the job. The evolution of hashing has seen a continuous push for faster execution, better statistical properties, and improved collision resistance, especially for pathological inputs.

Comparison with Other Non-Cryptographic Hash Functions

Let's compare Murmur Hash 2 with some other prominent non-cryptographic hash functions:

1. FNV (Fowler–Noll–Vo) Hash (e.g., FNV-1a):
   • Pros: Very simple to implement, extremely fast for small inputs, good general-purpose distribution.
   • Cons: Can be slower than Murmur Hash 2 for longer inputs, its mixing properties are less aggressive, making it slightly more susceptible to collisions with certain input patterns.
   • Versus Murmur Hash 2: Murmur Hash 2 generally offers superior statistical distribution and often better performance for larger data sets due to its more complex and aggressive mixing steps.
2. DJB2 Hash:
   • Pros: Extremely simple (often a single line of code), fast.
   • Cons: Known to have relatively poor distribution and higher collision rates compared to more sophisticated hashes. It's often used as a teaching example rather than for serious production use.
   • Versus Murmur Hash 2: Murmur Hash 2 is vastly superior in terms of distribution and collision resistance, making it a much more reliable choice for hash tables and similar applications.
3. CityHash:
   • Pros: Developed by Google, CityHash is highly optimized for short to medium-length strings and achieves exceptional speeds on modern processors, especially with SIMD instructions. It aims for high-quality distribution and collision resistance for its intended use cases. It supports different output sizes (64-bit, 128-bit).
   • Cons: More complex to implement than Murmur Hash 2, less suitable for very long strings where other hashes might perform better or be more robust.
   • Versus Murmur Hash 2: CityHash is often faster than Murmur Hash 2 for shorter inputs, and offers potentially better statistical properties. It's a strong successor or alternative, especially in modern Google environments.
4. xxHash (e.g., XXH32, XXH64):
   • Pros: An extremely fast hash function developed by Yann Collet, often boasting "near RAM speed" performance. It is highly optimized for modern CPUs, providing excellent distribution and collision resistance, even outperforming CityHash in many benchmarks. It is designed to scale well across different input sizes.
   • Cons: More complex than Murmur Hash 2 to implement from scratch.
   • Versus Murmur Hash 2: xxHash is generally considered to be a significant leap forward in non-cryptographic hashing, offering superior speed and often better statistical properties than Murmur Hash 2 across a wide range of input lengths. It has largely supplanted Murmur Hash 2 in new projects where the absolute fastest non-cryptographic hash is desired.
5. CRC32 (Cyclic Redundancy Check):
   • Pros: Very fast, widely implemented, excellent for detecting accidental data corruption (burst errors).
   • Cons: Not designed as a general-purpose hash function for unique identification; very weak collision resistance for general data (easy to find distinct inputs with the same CRC32 value), poor distribution for hash tables.
   • Versus Murmur Hash 2: CRC32 serves a different primary purpose (error detection). While fast, its hash distribution and collision resistance are far inferior to Murmur Hash 2 for applications like hash tables.

The Successor: Murmur Hash 3

It's also essential to acknowledge Murmur Hash 3, the direct successor to Murmur Hash 2, also developed by Austin Appleby. Murmur Hash 3 builds upon the strengths of Murmur Hash 2 and introduces several improvements:

• Improved Performance: Generally faster than Murmur Hash 2, especially on 64-bit platforms and for very long keys, due to further optimization of its mixing operations.
• Better Distribution and Collision Resistance: Offers even better statistical properties and stronger resistance to collisions, including some forms of adversarial attacks that might affect Murmur Hash 2.
• Wider Output Sizes: Murmur Hash 3 supports 32-bit and 128-bit outputs, providing more flexibility for different application requirements. The 128-bit variant provides an even larger hash space, further reducing the probability of accidental collisions.
• Standardization: Murmur Hash 3 has gained significant adoption and is considered a modern, robust general-purpose non-cryptographic hash.

While Murmur Hash 3 has largely superseded Murmur Hash 2 in new development, Murmur Hash 2 remains highly relevant due to its existing widespread deployments, its simplicity, and its excellent performance-to-quality ratio for its intended use cases. It’s a testament to its solid design that it continues to be a viable and effective choice in many scenarios, especially where compatibility with existing systems or a slightly simpler implementation is preferred over the absolute bleeding edge of hashing performance.

The choice of hashing algorithm depends heavily on specific requirements: the length of inputs, the desired speed, the acceptable collision rate, and the platform. Murmur Hash 2 carved out a crucial niche and paved the way for even faster and more robust non-cryptographic hashes like xxHash and Murmur Hash 3, solidifying its legacy as a foundational algorithm in the pursuit of efficient data management.

Comparative Analysis of Non-Cryptographic Hash Functions

Feature / Hash Function	Murmur Hash 2	FNV-1a	xxHash (XXH64)	CRC32
Primary Goal	Speed, good distribution for non-cryptographic uses	Simplicity, decent distribution	Extreme speed, excellent distribution	Error detection, speed
Speed (Relative)	Very Fast	Fast (esp. short inputs)	Extremely Fast (Near RAM speed)	Very Fast
Distribution Quality	Excellent	Good	Excellent	Poor (for hash tables)
Collision Resistance	Good (non-cryptographic)	Fair	Very Good (non-cryptographic)	Very Poor
Implementation Complexity	Moderate	Simple	Moderate	Moderate
Typical Output Size	32-bit, 64-bit	32-bit, 64-bit	32-bit, 64-bit	32-bit
Use Cases	Hash tables, Bloom filters, cache keys, data partitioning	Hash tables, unique IDs, simple checksums	Hash tables, distributed systems, cache keys, game engines	Error checking in data transmission, file systems
Cryptographically Secure?	No	No	No	No
Successor/Evolution	Murmur Hash 3	-	-	CRC32C (Castagnoli)

This table clearly illustrates that while Murmur Hash 2 remains a strong contender for many applications, newer options like xxHash often provide superior performance and distribution for modern systems. However, its ease of use, widespread existing deployments, and proven reliability ensure its continued relevance.

Conclusion

In the intricate tapestry of modern software architecture, hash functions like Murmur Hash 2 represent critical threads that contribute significantly to the overall strength, efficiency, and responsiveness of countless systems. Throughout this comprehensive exploration, we have delved into the profound impact of hashing on computing, understanding its fundamental principles, and tracing the ingenious design and evolution of Murmur Hash 2. We've seen how its meticulous blend of speed, achieved through carefully chosen bitwise operations and multiplications, and its exceptional statistical distribution have positioned it as a cornerstone for non-cryptographic applications, powering everything from efficient data structures like hash tables and Bloom filters to the complex load balancing and data partitioning strategies in sprawling distributed systems.

The brilliance of Murmur Hash 2 lies in its ability to consistently and quickly transform arbitrary data into compact, unique fingerprints, enabling rapid identification, indexing, and verification. While newer algorithms like Murmur Hash 3 and xxHash continue to push the boundaries of performance and collision resistance, Murmur Hash 2's proven track record, ease of implementation, and widespread adoption cement its legacy as a highly relevant and reliable choice for a vast array of tasks where cryptographic security is not a requirement. It exemplifies how thoughtful algorithmic design can yield enduring value in the pursuit of optimized computing.

Furthermore, we've highlighted the transformative power of accessibility offered by online tools. The "Murmur Hash 2 Online: Fast & Free Hash Calculator" democratizes access to this powerful algorithm, providing an invaluable resource for developers, system administrators, data analysts, and students alike. It eliminates the barriers of software installation and complex programming, delivering instant hash computations directly to a web browser. This convenience streamlines workflows, facilitates learning, and empowers a broader audience to leverage the efficiency of Murmur Hash 2 for quick verifications, prototyping, and troubleshooting. However, this convenience comes with the vital caveat of responsibility: the importance of never inputting sensitive information into online tools and always understanding the non-cryptographic nature of Murmur Hash 2.

Ultimately, Murmur Hash 2 stands as a testament to the continuous innovation in algorithm design, demonstrating how a focus on speed and distribution can unlock profound efficiencies across the digital landscape. As data volumes continue to explode and system complexity grows, the demand for fast, reliable, and accessible hashing solutions will only intensify. The legacy of Murmur Hash 2, both as a standalone algorithm and as a foundational stepping stone for its successors, underscores its enduring importance in shaping the future of high-performance computing.

---

Frequently Asked Questions (FAQ)

1. What is Murmur Hash 2 and how is it different from other hashes like MD5 or SHA-256? Murmur Hash 2 is a non-cryptographic hash function designed for high speed and excellent statistical distribution. It's primarily used for tasks like hash tables, Bloom filters, and cache keys where fast lookups and even data distribution are crucial. It differs from MD5 or SHA-256 in that the latter are cryptographic hash functions. Cryptographic hashes prioritize security, making it extremely difficult to reverse the hash or find collisions maliciously. Murmur Hash 2 does not offer this level of security and is susceptible to collision attacks, making it unsuitable for applications requiring cryptographic strength (like password storage or digital signatures).

2. Why should I use an "Online Murmur Hash 2 Calculator" instead of a local tool or programming it myself? An online calculator offers unparalleled convenience and accessibility. It requires no software installation or programming knowledge, making it ideal for quick checks, verifications, and learning. You can access it instantly from any device with an internet connection and a web browser. For developers, it's great for prototyping or debugging. For students, it's an interactive way to understand hashing. However, for sensitive data or production systems, a local, self-controlled implementation is always recommended.

3. Is Murmur Hash 2 still relevant, given the existence of Murmur Hash 3 and xxHash? Yes, Murmur Hash 2 remains relevant. While Murmur Hash 3 and xxHash offer improved performance and statistical properties, especially on modern 64-bit systems, Murmur Hash 2 has a long history of widespread adoption in numerous projects (e.g., Hadoop, Cassandra). Its simplicity, established reliability, and excellent performance-to-quality ratio mean it's still a perfectly viable and effective choice for many applications, particularly where compatibility with existing systems is a factor or where the absolute bleeding edge of hashing speed isn't strictly necessary.

4. Can I use Murmur Hash 2 to secure my passwords or verify important files? Absolutely not. Murmur Hash 2 is a non-cryptographic hash function, meaning it is not designed to withstand malicious attempts to find collisions or reverse the hash. Using it for password storage would make your system vulnerable to security breaches. For passwords, always use strong, slow cryptographic hashing functions like Argon2, bcrypt, or scrypt. For verifying important files against tampering, use cryptographic hashes like SHA-256 or SHA-3.

5. What factors can affect the output of a Murmur Hash 2 online calculator for the same input string? The most critical factor is the exact input string, including any leading/trailing whitespace, invisible characters, and line endings (e.g., "hello" is different from "hello "). The character encoding used by the calculator (e.g., UTF-8 vs. ASCII) can also change the hash value significantly for multi-byte characters. Additionally, if the calculator allows for a seed value, using a different seed will produce a different hash for the same input. Ensure consistency across these parameters for reproducible results.

🚀You can securely and efficiently call the OpenAI API on APIPark in just two steps:

Step 1: Deploy the APIPark AI gateway in 5 minutes.

APIPark is developed based on Golang, offering strong product performance and low development and maintenance costs. You can deploy APIPark with a single command line.

curl -sSO https://download.apipark.com/install/quick-start.sh; bash quick-start.sh

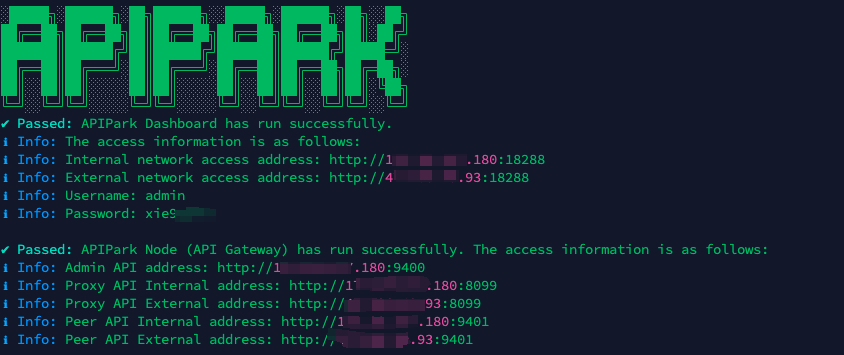
In my experience, you can see the successful deployment interface within 5 to 10 minutes. Then, you can log in to APIPark using your account.

Step 2: Call the OpenAI API.